................................................


№1
а) √50 > 7
√50 > √7²
√50 > √49
б) 4√6 > 3√7
√4²*6 > √3²*7
√16*6 > √9*7
√96 > √63
№2
а) √(196 * 0,64) = √(14²*(0,8)²) = 14 * 0,8 = 11,2
б) √(72*0,5)=√36=√6² = 6
в) 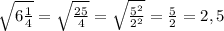
г) √(-2)⁶ = √((-2)³)²=(-2)³= - 8
№3
а) (√3+√2)² = (√3)²+ 2 *√3*√2 + (√2)²= 3 + 2√6 + 2 = 5 +2√6
б) (4 - √5)(4 + √5) = 4² - (√5)² = 16 - 5 = 11
в) 5√12 - 2√27 - 3√3 = 5√(4*3) - 2√(9*3) - 3√3 = 5√(2²*3) - 2√(3²*3) - 3√3 = 5*2√3 - 2*3√3 - 3√3= 10√3 - 6√3 - 3√3 = √3
№4
√(72*а⁵) = √(36*2 * а⁴*а)= √(6²*2 * (а²)² * а) = 6*а²*√(2а)
№5
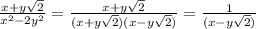
№6
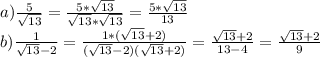
функцию можно записать так: y = (1 / 3)x - 4x^(- 2) + √x.
воспользовавшись формулами:
(x^n)’ = n* x^(n-1) (производная основной элементарной функции).
(√x)’ = 1 / 2√x (производная основной элементарной функции).
(с * u)’ = с * u’, где с – const (основное правило дифференцирования).
(u + v)’ = u’ + v’ (основное правило дифференцирования).
таким образом, производная нашей функции будет следующая:
y' = (x / 3 – 4 /x ^2 + √x)’ = ((1 / 3)x - 4x^(- 2) + √x)’ = ((1 / 3)x)’ – (4x^(- 2))’ + (√x)’ = (1 / 3 ) – (4 * (- 2) * x^(- 2 - 1)) + (1 / 2√x) = (1 / 3 ) + 8x^(- 3)) + (1 / 2√x) = (1 / 3 ) + (8 / x^3) + (1 / 2√x).
ответ: y' = (1 / 3 ) + (8 / x^3) + (1 / 2√x).
Вот решение.( ◜‿◝ )♡
Удачи!