Объяснение:
Найти площадь фигуры, ограниченной линиями:
у=х² +6х+12; х=-1; х=-3; у = 0
Построим указанные кривые на координатной плоскости
у=х² +6х+12 - уравнение параболы. Однозначно строится по трем точкам. Вершина параболы находится в точке с координатами(-3;3).
Еще две точки найдем подставив координаты х = -1 и х = -3 в уравнение параболы
у(-3) = 9 - 18 + 12 = 3
у(-1) = 1 - 6 + 12 = 7
Координаты двух других точек (-3;3) и (-1;7)
Уравнения х=-1; х=-3 на координатной плоскости описывают прямые.
Данные прямые параллельны оси абсцисс и проходят через точки (-1;0) и (-3;0) соответственно.
Прямая y=0 является осью ординат.
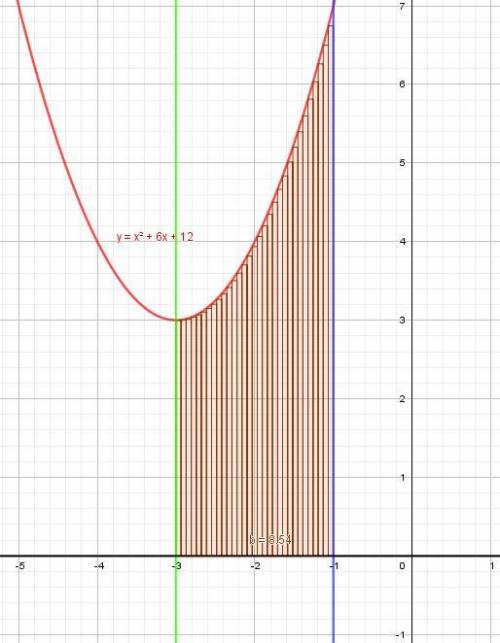
Фигура внутри полученного пересечения снизу ограничена прямой y=0 справа ограничена прямой х = -1, слева прямой х=-3, а сверху ограничена параболой у=х² +6х+12
Для нахождения площади фигуры найдем интеграл с пределами интегрирования от -3 до -1 и функцией х² +6х+12
![S = \int\limits^{-1}_{-3} {(x^2+6x+12)} \, dx=\frac{x^3}{3}+3x^2+12x\left[\begin{array}{ccc}-1&\\-3\end{array}\right] = \frac{-1}{3}+3-12-(-\frac{27}{3}+27-36)= -\frac{1}{3}-9 +18 = 9-\frac{1}{3} = 8,67](/tpl/images/1347/0292/7979d.png)
Объяснение:
Найти площадь фигуры, ограниченной линиями:
у=х² +6х+12; х=-1; х=-3; у = 0
Построим указанные кривые на координатной плоскости
у=х² +6х+12 - уравнение параболы. Однозначно строится по трем точкам. Вершина параболы находится в точке с координатами(-3;3).
Еще две точки найдем подставив координаты х = -1 и х = -3 в уравнение параболы
у(-3) = 9 - 18 + 12 = 3
у(-1) = 1 - 6 + 12 = 7
Координаты двух других точек (-3;3) и (-1;7)
Уравнения х=-1; х=-3 на координатной плоскости описывают прямые.
Данные прямые параллельны оси абсцисс и проходят через точки (-1;0) и (-3;0) соответственно.
Прямая y=0 является осью ординат.
Фигура внутри полученного пересечения снизу ограничена прямой y=0 справа ограничена прямой х = -1, слева прямой х=-3, а сверху ограничена параболой у=х² +6х+12
Для нахождения площади фигуры найдем интеграл с пределами интегрирования от -3 до -1 и функцией х² +6х+12
4 а 3 б 2 а
Объяснение:
вт ответ