2.
Общее число партий сыгранных между англичанами и немцами, французами и немцами, англичанами и французами можно найти двумя
Пусть число французов - 
Число англичан -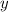 
Число немцев - 
Число партий вида: англичане - немцы
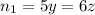
Число партий вида: англичане- французы
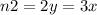
Число партий вида: немцы - французы
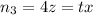, где 
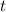- неизвестное число французов, что нужно найти.
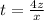
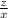можно определить поделив уравнение 1 (англичане - немцы) на уравнение 2 (англичане- французы) :
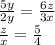
Таким образом :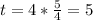 
ответ: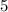 
1.
Это уравнение можно переписать в виде:
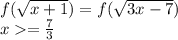
Где: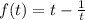 
Нетрудно убедиться, что при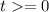 
(радикалы неотрицательны) данная функция монотонно возрастет.
Действительно, ведь производная данной функции положительна.
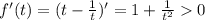
А поскольку функция монотонна, то одинаковые значения функции могут быть только у одинаковых значений аргумента.
То есть из уравнения:
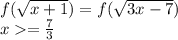
Следует равносильное ему уравнение:
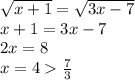
ответ: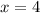 
sin (5πx/9) = sin (πx/9) + sin (2πx/9)
sin (5πx/9) - sin (πx/9) = sin (2πx/9)
По формуле разности синусов:
2sin(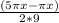
)cos(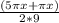
) - sin (2πx/9) = 0;
2 sin(2πx/9)cos(πx/3) - sin(2πx/9)=0;
sin (2πx/9) (2cos(πx/3)-1)=0;
sin (2πx/9)=0 или 2cos (πx/3)=1; cos (πx/3)=1/2
2πx/9=πn, n∈Z или πx/3=π/3+2πn, n∈Z или πx/3=-π/3+2πn, n∈Z;
Сокращаем на π:
2x/9=n, n∈Z или x/3=1/3+2n, n∈Z или x/3=-1/3+2n, n∈Z;
x=9n/2 или x=6n+1 или x=6n-1
Теперь отбираем корни уравнения, принадлежащие промежутку (4;8)
4<(9/2)n<8; 8/9<n<16/9; n=1, x=4,5
4<6n+1<8; 3<6n<7; 1/2<n<7/6; n=1; x=6+1=7;
4<6n-1<8; 5<6n<9; 5/6<n<3/2; n=1; x=6-1=5
ответ: x={4,5;5;7}
600
Объяснение:
Шестизначное число не может начинаться с 0, поэтому всего комбинаций первой цифры - 5
Вторая цифра уже может содержать 0, но не может содержать ту, которую выбрали ранее, поэтому всего комбинаций - 5
Третье число не может содержать цифру, выбранную ранее, значит всего комбинаций - 4. Оставшиеся цифры находим также.
Итого: 5 * 5 * 4 * 3 * 2 * 1 = 600 комбинаций