РЕШЕНИЕ
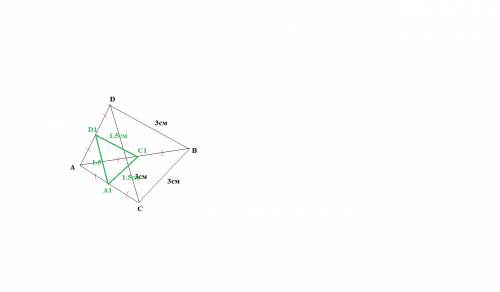
сделаем построение по условию
правильный тетраэдр - все грани правильный треугольник
правильный треугольник - все стороны равны b=3 см ; все углы равны =60 град
А1 ,D1,С1-средние точки на ребрах АС, AD,AB <---- можно расположить на любых ребрах - решение одинаковое
соединим точки А1 ,D1,С1
образовался новый треугольник A1D1C1
A1D1 -средняя линия треугольника ADC ; A1D1=DC/2=3/2=1.5
D1C1 -средняя линия треугольника ADB ; D1C1=DB/2=3/2=1.5
A1C1 -средняя линия треугольника ABC ; A1C1=BC/2=3/2=1.5
A1D1=D1C1= A1C1=a=1.5
периметр треугольника A1D1C1 P= A1D1+ D1C1+ A1C1=3*a=3*1.5=4.5
полупериметр p=P/2 =4.5/2=2.25
найти площадь A1D1C1 проще всего по формуле Герона
S=√(p*(p-a)(p-a)(p-a))= √(p*(p-a)^3)= √ (2.25*(2.25-1.5)^3)=√(1.5^2*0.75^2*0.5^2*3)
варианты ответов **на выбор
=√0.949219 см2
=0.974 см2
=0.97 см2
=0,5625√3 см2
ОТВЕТ 0,5625√3 см2 <---- этот я считаю самым АЛГЕБРАИЧЕСКИМ ))
x ∈{-2} ∪ [2;7]
Объяснение:
1) Найдём нули функции у₁ = х²-5х-14:
х²-5х-14 = 0
х₁,₂ = 5/2 ± √(25/4 +14) = 5/2 ± √(81/4) = 5/2 ± 9/2
х₁ = 5/2 + 9/2 = 14/2 = 7
х₂ = 5/2 - 9/2 = - 4/2 = -2
Графиком функции у₁ = х²-5х-14 является парабола, ветви которой направлены вверх; следовательно, у₁ = х²-5х-14 ≤0 на участке
x ∈ [-2; 7].
2) Неравенство х² ≥ 4 эквивалентно неравенству: х²- 4 ≥ 0.
Найдём нули функции у₂ =х²- 4:
х²- 4 = 0
х² = 4
х = ± √4
х₃ = - 2
х₄ = 2
Графиком функции у₂ = х²- 4 является парабола, ветви которой направлены вверх; функция у₂ = х²- 4 больше или равна нулю на участках:
x ∈(-∞; -2] ∪ [2;+∞)
3) Объединяем полученные решения, для чего на числовой оси отмечаем точки х₂ = -2; х₃ = -2; х₄ = 2; х₁ = 7 и находим перекрываемые области значений, одновременно удовлетворяющие неравенству х²-5х-14 ≤ 0 и неравенству х² ≥ 4:
x ∈{-2} ∪ [2;7]
ответ: x ∈{-2} ∪ [2;7]