Корней нет
Если проходите комплексные числа, то решение
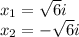
Объяснение:
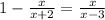перенесем выражение с неизвестной в правую часть и поменяем местами
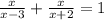приведем к общему знаменателю
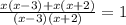домножим обе части на (х-3)(х+2) и сократим в левой части, добавив условие (х-3)(х+2) ≠0 ⇔ х ≠3 и х≠-2
x(х-3) + x(х+2) = (х-3)(х+2), раскроем скобки и сгруппируем
2х^2 - x = х^2 - x - 6, перенесем из правой части выражения содержащие переменную в левую со знаком минус и сгруппируем:
х^2 = -6
Корней нет
Если проходите комплексные числа, то решение
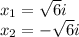
Последний карандаш окажется красный.