Условие. сумма второго и восьмого членов бесконечно убывающей геометрической прогрессии равна.325/128, а сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой же прогрессии. Найти первый член прогрессии и знаменатель.
Сумма второго и восьмого членов: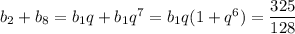 
Сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой прогрессии:
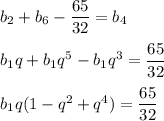
Из равенства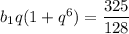 
заметим, что второй множитель можно разложить на множители по формуле суммы кубов
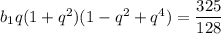
Подставляем данные, получим
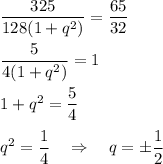
ответ: 5; 0.5 и -5; -0.5.
x = y+2
x²+y²=37
(y+2)²+y²=37
y²+2*2*y+2²+y²=37
2y²+4y+4=37
y²+2y+2=37 сократили на "2"
y²+2y-35=0
D(дискриминант) = 2²-4*1*(-35)=144
y₁ = -2-12 / 2 = -7
y₂ = -2+12 / 2 = 5.
x₁ = -7+2 = -5
x₂ = 5+2 = 7
(-7;5)(-5;7)