Треугольник получается равнобедренный, в котором АС и ВС - боковые стороны, АВ - основание.
Проведем высоту СЕ. У нас получится прямоугольный треугольник СЕА, где угол Е - прямой.
В равнобедренном треугольнике высота проведенная к основанию является и биссектрисой и высотой.
Значит ВЕ=ЕА
СЕ = СА*sinA = 25√(21)*0.4 = 10√(21)
Найдем ЕА = ВЕ по теореме Пифагора:
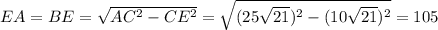
AB = 2 * 105 = 210
За формулой найдем АН:
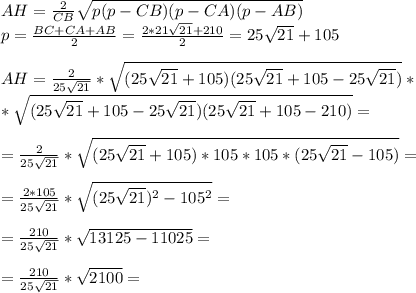
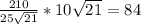
AH = 84
ответ: 1) ответ-нет.
На плоскости у двух прямых всего два варианта – прямые пересекаются или не пересекаются (параллельны). Если пересекаются, то имеют только одну общую точку.
2) ответ -нет
Через точку плоскости можно провести множество прямых, не принадлежащих данной плоскости.
Через точку плоскости можно провести множество прямых, на данной плоскости.
3) ответ-нет.
Если две прямые пересекаются, то делят плоскость на 4 части
Если две прямые параллельны, то они делят плоскость на 3 части.
4) ответ-нет.
Точка, делящая отрезок на две равные части, называется серединой отрезка.
5) ответ-нет
Если точки A, B, C лежат на одной прямой, причём точка В лежит между точками А и С, то имеет место равенство: AB+BC=AC
В решении.
Объяснение:
Решить неравенство:
1) 3(х + 4) + 2(3х - 2) > 5х - 3(2х + 4)
Раскрыть скобки:
3х+12+6х-4 > 5х-6х-12
Привести подобные члены:
9х+х > -12-8
10х > -20
х > -20/10
х > -2
x∈(-2; +∞) ответ а)
Неравенство строгое, скобки круглые.
2) 2х - 6 - 5(2 - х) <= 12 - 5(1 - x)
Раскрыть скобки:
2х-6-10+5х <= 12-5+5х
Привести подобные члены:
7х-5х <= 7+16
2х <= 23
x <= 23/2
x <= 11,5
х∈(-∞; 11,5] ответ б)
Неравенство нестрогое, скобка квадратная, а знаки бесконечности всегда с круглыми скобками.
3) х + 2 < 5(2х + 8) + 13(4 - х) - 3(х - 2)
Раскрыть скобки:
х+2 < 10х+40+52-13х-3х+6
Привести подобные члены:
х+6х < 98-2
7х < 96
х < 96/7
x < 13 и 5/7
х∈(-∞; 13 и 5/7) ответ в)
Неравенство строгое, скобки круглые.
1) Треугольник получается равнобедренный, в котором АС и ВС - боковые стороны, АВ - основание.
Проведем высоту СН. У нас получится прямоугольный треугольник СНА, где угол Н - прямой.
В равнобедренном треугольнике высота проведенная к основанию является и биссектрисой и высотой.
Значит ВН=НА=16/2=8
Далее по теореме Пифагора находим СН.
СН = кв. корень (10*10-8*8) = 6
Синус А = СН/СА = 6/10 = 3/5
2) Треугольник получается равнобедренный, в котором АС и ВС - боковые стороны, АВ - основание.
Проведем высоту СН. У нас получится прямоугольный треугольник СНА, где угол Н - прямой.
В равнобедренном треугольнике высота проведенная к основанию является и биссектрисой и высотой.
Значит ВН=НА
СН = СВ*СинусВ = 10*0,8 = 8
ВН=НА=кв.корень (10*10-8*8) = 6
АВ = ВН+НА = 6+6 = 12
Всё правильно