1) a - (2;1), б - (-2;-1) 2)y = 7x - 8 3) (1/3;1/2);
Объяснение:
1) a) { 3x - 2y = 4 б){ 2x - 7y = 3
{ 5x + 2y = 12 { 3x + 4y = -10
Сложим: Домножим первое уравнение на -1.5
3x+5x-2y+2y=16 {-3x+10,5y=-4,5
8x=16 {3x+4y=-10
x=2 Сложим:
Подставим в первое уравнение: 14,5y = -14,5
3*2 - 2y = 4 y = -1
-2y = 4 - 6 Подставим в первое:
-2y = -2 2x + 7 = 3
y = 1 2x = -4
ответ: (2;1) x=-2
ответ: (-2;-1)
2) Функция проходит через точки (2;6) и (1;-1), а значит можно подставить эти значения в формулу функции:
{6 = 2k+ b
{-1 = 1k + b
Домножим второе на -2:
{6 = 2k+b
{2 = -2k - 2b
Сложим:
6 + 2 = 2k - 2k - 2b + b
-b = 8
b = -8
Подставим в второе уравнение:
-1 = k - 8
k = 7
Получаем функцию: y = 7x-8
3) Сделаем замену 1/x = a; 1/y = b, тогда:
{a + b = 5
{5a - 2b = 11
Умножим первое уравнение на 2:
{2a + 2b = 10
{5a - 2b = 11
Сложим:
2a + 5a + 2b - 2b = 10+11
7a = 21
a = 3
Подставим в первое уравнение:
3 + b = 5
b = 2
Делаем обратную замену:
1/x = 3 1/y = 2
x = 1/3 y = 1/2
1)
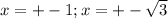2) 2 км/ч
Объяснение:
1) Не биполярное, а биквадратное, Сделаем замену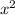
= t, тогда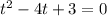 
D = 4*4 - 4 * 3 = 4 = 2*2
t1 = (4-2)/2 = 1
t2 = (4+2)/2 = 3
Делаем обратную замену:
x = -1; x = 1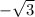; x=
;x=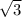
2) Пусть x - скорость течения Так как обратно он смог вернутся на плоту, то тогда он плыл по течению, значит изначально он плывет против течения со скоростью 12 - x, а затратил он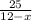
часов.
Плывя на плоту он потратил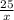
часов, но еще из условия известно, что время на лодке = время на плоту - 10, т.е
Домножим на x(12-x):
Раскроем скобки:
Перенесём в правую часть и приведем подобные слагаемые: