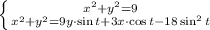
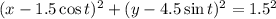, видим, что решениями системы есть координаты точек пересечений кругов с центрами 
и 
и 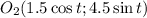радиусам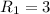и 
и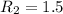 
согласно. Эти круги имеют единую общую точку в таких случаях
(внешний ощупь)
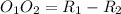(внутренний ощупь)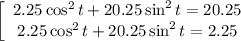
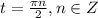. Остается при этих значениях параметра t решить систему уравнений.
решение системы будет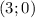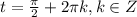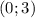 
решение системы: 
решение системы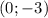 
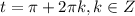, решение системы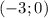 
Чтоб проверить проходит ли график уравнения через точку, нужно, значение точки подставить в уравнение.
а) А(3; 1), 3х + 4у = 2,
3 * 3 + 4 * 1 = 2;
9 + 4 = 2;
13 ¥ 2. (¥ - не равно)
Значит, график уравнения не проходит через данную точку.
б) В(2; 1), 3х + 4у = 2,
3 * 2 + 4 * 1 = 2;
6 + 4 = 2;
10 ¥ 2.
Значит, график уравнения не проходит через данную точку.
в) С(- 2; - 2), 3х + 4у = 2,
3 * (- 2) + 4 * (-.2) = 2;
- 6 - 8 = 2;
- 14 ¥ 2.
Значит график уравнения не проходит через данную точку.
ответ: точки не принадлежат графику