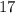 и
и  – среднеарифметическое равно
– среднеарифметическое равно  и при этом
и при этом  на
на  меньше двадцати пяти и на
меньше двадцати пяти и на  больше семнадцати.
больше семнадцати. монет и у них становится поровну, то они как раз и приходят к среднеарифметическому их начальных количеств монет. В итоге у Васи оказывается на
монет и у них становится поровну, то они как раз и приходят к среднеарифметическому их начальных количеств монет. В итоге у Васи оказывается на  монет меньше изначального, а у Пети на
монет меньше изначального, а у Пети на  монет больше изначального. А значит, вначале у Васи было на
монет больше изначального. А значит, вначале у Васи было на 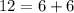 монет больше, чем у Пети.
монет больше, чем у Пети. монет. Тогда у Пети
монет. Тогда у Пети  монет.
монет.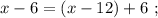
 монет, а у Пети-II будет
монет, а у Пети-II будет  монет. При этом у Пети-II монет в
монет. При этом у Пети-II монет в 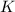 раз меньше, т.е. если мы количество монет Пети-II мысленно увеличим в
раз меньше, т.е. если мы количество монет Пети-II мысленно увеличим в 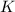 раз, то их станет столько же, сколько и у Васи-II. На этом основании составим уравнение:
раз, то их станет столько же, сколько и у Васи-II. На этом основании составим уравнение:

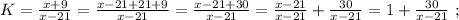

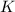 было целым, целой должен быть и результат деления в дроби, а чтобы
было целым, целой должен быть и результат деления в дроби, а чтобы 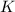 было максимальным, частное от деления в дроби должно быть максимальным, а значит её знаменатель должен быть минимальным, целым, положительным числом, что возможно только, когда
было максимальным, частное от деления в дроби должно быть максимальным, а значит её знаменатель должен быть минимальным, целым, положительным числом, что возможно только, когда 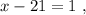 откуда:
откуда:
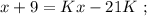

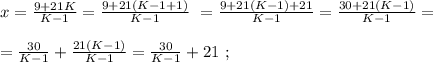
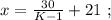
 было целым, целой должен быть и результат деления в дроби. А максимальное значение знаменателя в такой дроби (при том, что частное от деления остаётся целым) составляет
было целым, целой должен быть и результат деления в дроби. А максимальное значение знаменателя в такой дроби (при том, что частное от деления остаётся целым) составляет 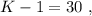 откуда:
откуда:
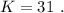
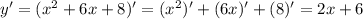
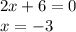
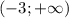 , а убывает -
, а убывает - 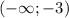
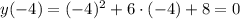
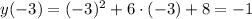 - наименьшее
- наименьшее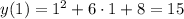 - наибольшее
- наибольшее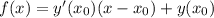
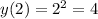
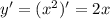
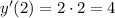
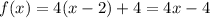
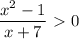
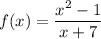
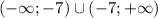
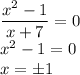
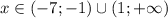
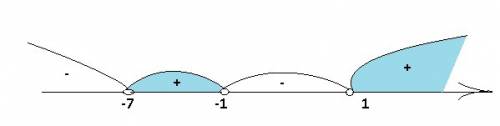
Задачи "на трубы" или "совместную работу" совершенно идентичны задачам "на движение", главную роль в них всегда играет скорость (движения, истечения жидкости, работы(т.н. производительность труда)). Всегда ориентируйся на эти аналогии и любая задачка будет очень просто решаться. Смотри.
Пусть
Va - скорость истечения воды из трубы а,
Vb - из трубы b, ну и
(Va+Vb) - скорость наполнения, если обе трубы открыты.
Вот, по сути, и всё. Дальше совсем просто.
Пусть объём всего чана равен Ч(можно положить равным 1, Ч потом сократится, но пусть будет Ч).
Так как время это расстояние(у нас объём) на скорость, то первое предложение задачи запишется так
Ч/(Va+Vb) = 6, откуда
(Va+Vb) = Ч/6.
Далее рассмотрим второе предложение.
За четыре часа совместной работы воды нальётся
(Va+Vb)*4 = Ч/6 * 4 = (2/3)*Ч.
А останется заполнить
Ч - (2/3)*Ч = Ч/3. И этот объём заполняет только труба b, то есть она заполнит этот объём за
(Ч/3)/Vb = Ч/(3*Vb) = 5, откуда
Vb = (1/15)*Ч, но ведь
Va+Vb = Ч/6, то есть
Va = Ч/6 - Vb = Ч/6 - Ч/15 = Ч/10
Всё! Задача решена, нам известны скорости истечения жидкости из каждой из труб, поэтому
Труба а заполнит весь чан за
Ч/Va = Ч/(Ч/10) = 10, ну а труба b за
Ч/Vb = Ч/(Ч/15) = 15. (это по условию находить не нужно, ну да ладно, мы заодно и это найдём).
Всё! Задача решена!
ответ
Труба а заполнит весь чан за 10 часов, а труба b за 15 часов.