Варфитической прогрессии (аn) a1=5, d=4. найдите сумму всех членов этой прогрессии с 20-ого по 30-й - id142878320211205 от anyanaffanya 05.12.2021 18:08

Question

Алгебра: Варфитической прогрессии (аn) a1=5, d=4. найдите сумму всех членов этой прогрессии с 20-ого по 30-й включительно.

anyanaffanya · Accepted Answer

Нужно найти наименьшее натуральное число, которое при умножении на 2 даст полный квадрат, а при умножении на 3 - полный куб.
Обозначим искомое число за

. Любое число можно представить в виде произведения простых множителей. Запишем:
x = 2^n * 3^m*k

, где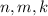

- некоторые натуральные числа.
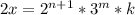По условию, число $2x = 2^{n+1}*3^m*k$ является полным квадратом, значит n+1

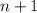и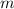

- четные числа, а

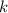- полный квадрат. Аналогично, число 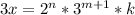$3x = 2^n*3^{m+1}*k$ является полным кубом, значит

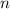и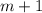

делятся на 3, а

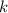- полный куб.
Легко видеть, что наименьшие возможные значения n,m,k

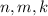это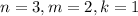

, значит

.

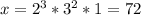Варфитической прогрессии (аn) a1=5, d=4. найдите сумму всех членов этой прогрессии с 20-ого по 30-й включительно.

MOGZ ответил