пусть x- одна сторона прямоугольника
пусть у- вторая сторона прямоугольника
составляем систему уравнений
у=5+x
xy=84
из этого следует
x(5+x)=84
5x+x2=84
x2+5x-84=0
а теперь несколько решения этого уравнения 2 самых частых это через дискриминант
д=25+336=361
x1,2=(-5+-19)/2
x1=14/2=7
x2=-24/2=-12
или методом выделения полного квадрата
x2+5x=84
(x+2,5)^2=90,25
x+2,5=9,5или x+2,5=-9,5
x=7или x=-12
в обоих случаях x =7 и х=-12 но так как сторона не может быть отрицательным числом -12 не может быть
y=7+5=12
ответ:x=7 y=12
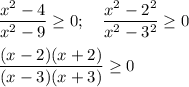
Решим неравенство методом интервалов.
Отмечаем на координатной прямой точки, в которых знаменатель и числитель обращаются в ноль. И выкалываем те, что из знаменателя. Мы получили 5 интервала. Перед дробью знак положительный и все множители имею пол. знак при х, поэтому на правом интервале ставим "плюс", далее чередуем знак через каждую отмеченную точку (все множители в нч степени - 1). Нас интересует, когда больше или равно, поэтому выбираем интервалы с плюсом, учитывая границы.
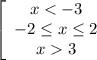
ответ: x ∈ (-∞;-3) ∪ [-2;2] ∪ (3;+∞).
В решении использовалась формула сокращённого умножения: a²-b²=(a-b)(a+b).

s= 5* x = 84 => x = 16.8
ab= 5
bc= 16.8
cd= 5
ad= 16.8