Объяснение:
вынесем за скобки общие множители
x²-5x+6+[√(a(x-2))](x=3)-6a(x-3)=0 (1)
x²-5x+6 разложим на множители
х₁=-2;x=3 нашел подбором с использованием теоремы Виета
1. при а=0 выражение (1) принимает вид x²-5x+6=0 и имеет два решения
по формуле ax²+bx+c=a(x-x₁)(x-x₂)
x²-5x+6=(x+2)(x-3) подставим в (1)
(x+2)(x-3)+[√(a(x-2))](x=3)-6a(x-3)=0 вынесем за скобки общий множитель
(x-3)(x+2)+[√(a(x-2))]-6a)=0 это выражение имеет решение х=3
очевидно что, чтобы выражение (1) имело единственное решение выражение x+2+[√(a(x-2))]-6a=0 (2) не должно иметь решений
преобразуем выражение (2)
√(a(x-2))=-х+(6a-2) решим это уравнение графическим
у=√(a(x-2))
у=-х+(6a-2)
чтобы уравнение (2) не имело решений надо найти такое а при котором графики указанных выше функций не пересекались
выясним взаимное расположение графиков в зависимости от параметра а
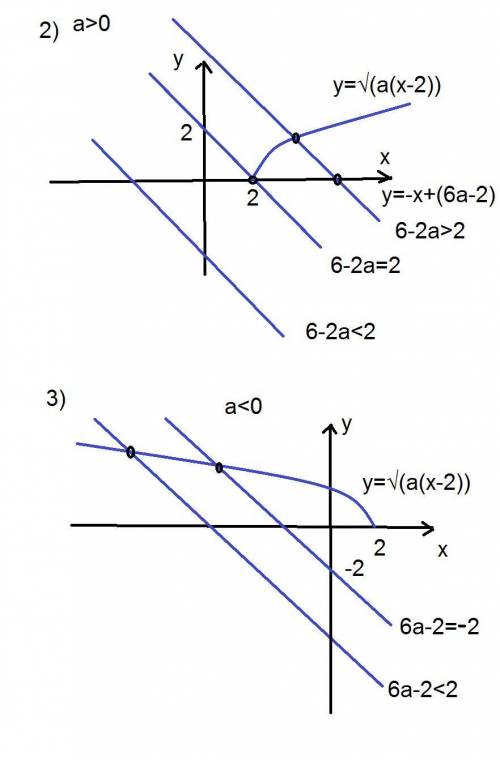
2. При а>0
графиком у=√(a(x-2)) является кривая линия получающаяся из линии у=√х переноса вдоль оси ОХ на 2 единицы вправо и сжатием - растяжением вдоль оси ОХ в зависимости от значения а
крайняя левая по оси ОХ точка кривой (2;0) , ветка кривой направлена вправо .
так как a>0 (6a-2)>-2
2.1. при (6a-2)=2 прямая у=-х+(6a-2) имеет вид у=-х+2 и проходит через точку (2;0) и графики пересекаются в этой точке, при этом (2) имеет одно решение
2.2 при 6a-2>2 прямая у=-х+(6a-2) находится выше прямой у=-х+2 и и графики пересекаются в двух точках при этом (2) имеет 2 решения
2.3 при 6a-2<2 прямая у=-х+(6a-2) находится ниже прямой у=-х+2 и и графики не пересекаются (2) не имеет решений
при этом
6a-2<2 ; 6a<4; a<4/6; a<2/3 с учетом того что мы рассматриваем a>0
0<a<2/3
3. При а<0
графиком у=√(a(x-2)) является кривая линия получающаяся из линии у=√х переноса вдоль оси ОХ на 2 единицы вправо и сжатием - растяжением вдоль оси ОХ в зависимости от значения а
крайняя правая относительно оси ОХ точка кривой (2;0) , ветка кривой направлена влево .
так как a<0 то (6a-2)<-2
так как (6a-2)<-2
прямая у=-х+(6a-2) в этом случае находится ниже прямой у=-х-2
которая имеет с графиком кривой общую точку и тоже имеет с графиком кривой общую точку
в этом случае (2) имеет решение
таким образом, уравнение 1 имеет единственное решение
при 0<a<2/3
a) (x²-1)(x-2)(x+3)≤ 0
(x-1)(x+1)(x-2)(x+3)≤0
-3-112
+ - + - +
x∈[-3; -1]∪[1; 2]
б) (x²-25)(x-2)(x-4)≥0
(x-5)(x+5)(x-2)(x-4)≥0
-5245
+ - + - +
x∈(-∞; -5] ∪[2; 4]∪[5; +∞)
в) (x²-2x-8)(x+5)≤ 0
(x²-4x+2x-8)(x+5)≤ 0
(x(x-4)+2(x-4))(x+5)≤ 0
(x+2)(x-4)(x+5)≤0
-5-24
- + - +
x∈(-∞; -5] ∪[2; 4]
г) (x²+2x-15)(x-1)≥ 0
(x²-3x+5x-15)(x-1)≥ 0
(x(x-3)+5(x-3))(x-1)≥ 0
(x-3)(x+5)(x-1)≥0
-513
- + - +
x∈[-5; 1]∪[3; +∞)
д) (x² -16)(x²+2x-8)(x-2)≤ 0
(x-4)(x+4)(x-2)(x+4)≤0
(x-4)(x+4)²(x-2)≤0
-424
+ + - +
x∈[2; 4]
е) (x²-9)(x²+x-6)(x+5)≥ 0
(x-3)(x+3)(x-1)(x+5)(x+5)≥0
(x-3)(x+3)(x-1)(x+5)²≥0
-5-313
- - + - +
x∈[-3; 1]∪[3; +∞)
2(3х+4) = 8х-(2х-5)
6х+8 = 8х-2х+5
6х-8х+2х = 5-8
0 = -3.
ответ: х ∈ ∅.