На
а) функция возрастает на всём промежутке, точек экстремума, соответственно, нет;
б) находишь производную (2х+4), приравниваешь её нулю, 2х+4=0, х=-2 - точка экстремума, подставляешь в уравнение производной пробные значения, при значениях меньше -2 ответ будет отрицательным, значит, функция убывает на данном промежутке. При значениях больше -2 ответ будет положительным, значит, функция возрастает на данном промежутке.
в) производная: 3х^2- 2х, приравниваешь нулю, находишь корни квадратного уравнения (-1/3 и 1) (они же будут являться точками экстремума), рисуешь числовую прямую, подставляешь пробные значения в уравнение производной, например -1; 0 и 2 и там (на тех промежутках), где ответ отрицательный- функция убывает, а где положительный- возрастает.
(см. объяснение)
Объяснение:
Т.к. ваш предыдущий вопрос был удален странным модератором, а я на него написал ответ, то даю ответ на тот вопрос в этом:
Понятно, что первые два корня - это 3 и -2.
Решим уравнение:
По тригонометрической теореме Виета:
Т.к.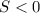 и
и 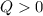 , то:
, то:
Тогда:
Уравнение решено!