
ответ: 1) 9x+13=6x+4
9x-6x+13=4
9x-6x=4-13
3x=4-13
3x=-9
x=-3
2) 9x=3+4(5x+2)
9x=3+20x+8
9x=11+20x
9x-20x=11
-11x=11
x=-1
3) 6+7(4x-3)=3x-65
6+28x-21=3x-65
-15+28x=3x-65
28x-3x=-65+15
25x=-50
x=-2
4) 5(4x+3)-7(4x-7)=24
20x+15-7(4x-7)=24
20x+15-28x+49=24
-8x+15+49=24
-8x+64=24
-8x=24-64
-8x=-40
x=5
5) 1-5(2x-5)-3(2-3x)=4x
1-10x+25-3(2-3x)=4x
1-10x+25-6+9x=4x
20-10x+9x=4x
20-x=4x
-x=4x-20
-x-4x=-20
-5x=-20
x=4
6) 2,1(2-x)+1,4(1,5x-3)=2
4,2-2,1x+1,4(1,5x-3)=2
4,2-2,1x+2,1x-4,2=2
0-2,1x+2,1x=2
0+0=2
0=2
Утверждение ложно для любого значения x x ε нет решения
9.
log₁₄ 7 = m найдем log₁₇₅ 56 - ?
log₁₄ 5 = n
Используем формулу перехода другому основанию:
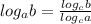
log₁₇₅ 56 = log₁₄ 56/log₁₄ 175 = log₁₄ (8×7)/log₁₄ (25×7) = log₁₄ (2³×7)/log₁₄ (5²×7) = log₁₄ 2³ × log₁₄ 7/log₁₄ 5² × log₁₄ 7 = 3log₁₄ 2 × log₁₄ 7/2log₁₄ 5 × log₁₄ 7
Нам нужно найти log₁₄ 2:
log₁₄ 2 = log₁₄ 14/7 = log₁₄ 14 - log₁₄ 7 = 1 - m
Получаем:
log₁₇₅ 56 = 3×(1 - m) + m/2n + m = 3 - 3m + m/2n + m = 3 - 2m/2n + m
ответ: log₁₇₅ 56 = 3 - 2m/2n + m
10.
log₅ 5 = 1
log₁₁ 15 = log₁₀ 15/log₁₀ 11 ≈ 1,17609/1,04139 ≈ 1,12934
Следовательно:
1 < 1,12934
log₅ 5 < log₁₁ 15
ответ: log₅ 5 < log₁₁ 15
Объяснение:
Тема: Итоговое повторение курса алгебры 10 класса
Урок: Арксинус и решение уравнения sinx=a
1. Введение. График функции y=sinx, x∈[-π/2;π/2]
На уроке рассматривается понятие функции арксинус, примеры на вычисление арксинусов по графику и на единичной окружности, решается уравнение при .
По теореме о существовании обратной функции прямая функция должна быть непрерывной и монотонной.
Функция не монотонна на всей своей области определения, а на промежутке она непрерывна, монотонна и пробегает все значения из области значений. Значит, существует обратная функция для нее на этом промежутке, она называется арксинус.
Построим график функции на отрезке (рис. 1) и будем находить значения арксинусов чисел по этому графику.
Объяснение: