СК=12
12=АС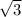
/2 => AC=8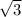
Sосн=48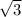
угол SKО=60
ОК=1/3СК
ОК=4
cos60=OK/SK
SK=8
Sтр.ASB=1/2*8*8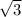=32
Sбок=32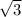*3=96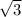
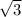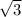Sпов=48+96=144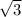
3) 20°
Объяснение:
Подсказка
Через точку C проведите прямую, параллельную MN, до пересечения с прямой AB в точке K. Треугольник ACK – равнобедренный.
Решение
Через точку C проведём прямую, параллельную MN, до пересечения с прямой AB в точке K. Поскольку M – середина BC и MN || CK, то отрезок MN – средняя линия треугольника BCK. Поэтому KN = BN, а так как N – середина AD, то AK = BD = AC. Значит, треугольник ACK – равнобедренный.
BAC – внешний угол равнобедренного треугольника ACK, поэтому ∠BNM = ∠BKC = ½ ∠BAC = 20°.
Использовано свойство катета против угла в 30 градусов, формулы высоты правильного треугольника, формула площади правильного треугольника, свойство центра правильного треугольника, формула площади полной поверхности пирамиды