функцию можно записать так: y = (1 / 3)x - 4x^(- 2) + √x.
воспользовавшись формулами:
(x^n)’ = n* x^(n-1) (производная основной элементарной функции).
(√x)’ = 1 / 2√x (производная основной элементарной функции).
(с * u)’ = с * u’, где с – const (основное правило дифференцирования).
(u + v)’ = u’ + v’ (основное правило дифференцирования).
таким образом, производная нашей функции будет следующая:
y' = (x / 3 – 4 /x ^2 + √x)’ = ((1 / 3)x - 4x^(- 2) + √x)’ = ((1 / 3)x)’ – (4x^(- 2))’ + (√x)’ = (1 / 3 ) – (4 * (- 2) * x^(- 2 - 1)) + (1 / 2√x) = (1 / 3 ) + 8x^(- 3)) + (1 / 2√x) = (1 / 3 ) + (8 / x^3) + (1 / 2√x).
ответ: y' = (1 / 3 ) + (8 / x^3) + (1 / 2√x).
Уравнение прямой, отсекающей от первого координатного угла треугольник, имеет вид y=kx+b . Этот треугольник прямоугольный и его площадь равна половине произведения катетов.
Так как точка А(1;2) принадлежит этой прямой,то подставив координаты точки А(1;2) в это уравнение получим
Уравнение прямой теперь будет выглядеть так: 
.
Найдём точки пересечения этой прямой с осями координат:
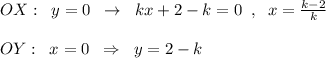
Длины отрезков, отсекаемых прямой y=kx+2-k на координатных осях, равны (2-k) на оси ОУ и (k-2)/k на оси ОХ. Эти отрезки и есть катеты прямоугольного треугольника. Вычислим его площадь:
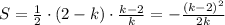
Найдём минимум это функции S(k).
Точка минимума: 
, так как при переходе через k= -2 производная меняет знак с минуса на плюс.
При k= -2 уравнение искомой прямой будет
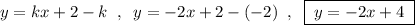
ответ: k= -2 .
ответ: x²
Объяснение:
(a³•x⁵)²/(a²)³•x⁸