ответ: 3 км/ч
Пошаговое решение:
Пусть собственная скорость равна х км/ч, тогда скорость против течения равна (x-1) км/ч, а по течению — (x+1) км/ч. Время, затраченное против течения, равно 6/(x-1) ч, а по течению — 6/(x+1) ч. На весь путь байдарка затратила 6/(x-1) + 6/(x+1) ч, что по условию составляет 4ч30мин.
4 ч 30 мин = 4 ч+ 30/60ч = 4,5 ч.
Составим и решим уравнение:
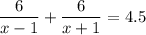
Для простоты умножим обе части уравнения на 2(x-1)(x+1)≠0
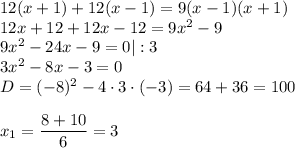
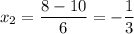 - не удовлетворяет условию
- не удовлетворяет условию
Собственная скорость байдарки составляет 3 км/ч.
x=12, min((16/x)+(x/9))=8/3
Объяснение:
Часть теоремы о средних - неравенство между средним арифметическим и средним геометрическим(неравенство Коши)
(16/x)+(x/9)≥2√((16/x)(x/9))=2√(16/9)=2·4/3=8/3
Равенство достигается при 16/x=x/9⇔x²=144⇔x=±12
x>0⇒x=12
min((16/x)+(x/9))=8/3
Можно решить и другим
Рассмотрим функцию f(x)=16/x+x/9 при x>0. Найдём промежутки её монотонности.
f '(x)=-16/x²+1/9=(x²-144)/(9x²)=(x-12)(x+12)/(9x²)
x∈(0;12)⇒f '(x)<0⇒f↓
x∈(12;+∞)⇒f '(x)>0⇒f↑
minf(x)=f(12)=16/12+12/9=4/3+4/3=8/3
x∈(0;+∞)