а) 2(х-3)=36. б)4(5-х)=12 в)0,1(х+1)=1 А) 4(х+1)+11=31 Б)16+3(z-2)=1
2х-6=36 20-4х=12 0.1х+0.1=1 4х+4+11=31 16+3z-6=1
2х=36+6 -4х=12-20 0.1х=1-0.1 4х=31-4-11 3z=1-16+6
2х=42 -4х=-8 0.1х=0.9 4х=16 3z= -9
х=21 х=2 х=9 х=4 z= -3
с) 3х+(7-х)=10 в) 8z-(5-3z)=17 д) 2х-(3-х)=18 г) 12у+(5-2у)=-15
3x+7-x=10 8z-5+3z=17 2x-3+x=18 12y+5-2y= -15
3x-x=10-7 8z+3z=17+5 2x+x=18+3 12y-2y= -15-5
2x=3 11z=22 3x=21 10y= -20
x=1.5 z=2 x=7 y= -2
1) Пусть cos x > 0, тогда |cos x| = cos x
sin x > √3*cos x - √2
Делим всё на 2.
1/2*sin x > √3/2*cos x - √2/2
√2/2 > √3/2*cos x - 1/2*sin x
√2/2 > cos x*cos(pi/6) - sin x*sin(pi/6)
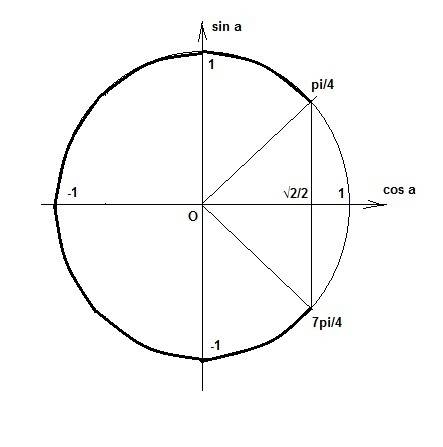
cos (x + pi/6) < √2/2
pi/4 + 2pi*k < x + pi/6 < 7pi/4 + 2pi*k
На 1 рис. показано, почему это так.
Интересующая нас часть круга выделена жирной линией.
pi/4 - pi/6 + 2pi*k < x < 7pi/4 - pi/6 + 2pi*k
3pi/12 - 2pi/12 + 2pi*k < x < 21pi/12 - 2pi/12 + 2pi*k
x ∈ (pi/12 + 2pi*k; 19pi/12 + 2pi*k)
С учетом условия cos x >= 0 получаем:
x ∈ (pi/12 + 2pi*k; pi/2 + 2pi*k] U [3pi/2 + 2pi*k; 19pi/12 + 2pi*k)
2) Пусть cos x < 0, тогда |cos x| = -cos x
sin x > -√3*cos x - √2
Делим всё на 2.
1/2*sin x > -√3/2*cos x - √2/2
√3/2*cos x + 1/2*sin x > -√2/2
cos x*cos(pi/6) + sin x*sin(pi/6) > -√2/2
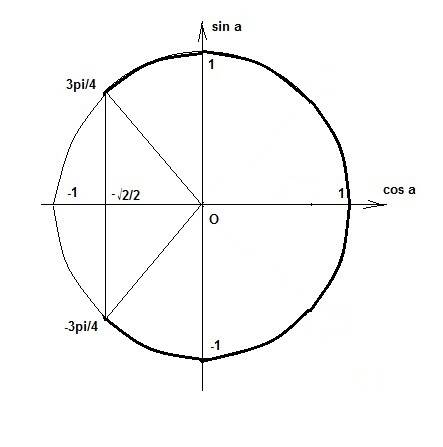
cos (x - pi/6) > -√2/2
-3pi/4 + 2pi*k < x - pi/6 < 3pi/4 + 2pi*k
На 2 рис. показано, почему это так.
-3pi/4 + pi/6 + 2pi*k < x < 3pi/4 + pi/6 + 2pi*k
-9pi/12 + 2pi/12 + 2pi*k < x < 9pi/12 + 2pi/12 + 2pi*k
x ∈ (-7pi/12 + 2pi*k; 11pi/12 + 2pi*k)
С учетом условия cos x < 0
x ∈ (-7pi/12 + 2pi*k; -pi/2 + 2pi*k) U (pi/2 + 2pi*k; 11pi/12 + 2pi*k)
Если свести оба случая в один ответ, то получится:
x € (-7pi/12 + 2pi*k; -5pi/12 + 2pi*k) U (pi/12 + 2pi*k; 11pi/12 + 2pi*k)
не знаю правильно или нет