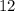ймовірність того, що листочок ммістить цифру 2 дорівнює проте ймовірність того, що листок містить саме число 2 менша та дорівнює
Объяснение:
У високостном році 366, є місяці по 31 денів по 30 днів та у лютому 29 днів
Тож подивимось скількі днів у місяці містять двійку:
це номери 2, 12, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29 - загалом це 12 днів на місяць,
як бачимо у кожному місяці високостного року по 12 днів із цифрою 2
тому на рік таких днів буде 12*12=144
а ймовірність такої події
--------------------------
якщо ж казати про можливість натрапити саме на число 2 на листочку то це лише , оскыльки других днів у році стількиж скіль ки ж і місяців у році, а саме
Решение: х²+2√(х²+19)=44 2√(х²+19)=44-х² Чтобы избавиться от иррациональности возведём обе части уравнения в квадрат: 4(х²+19)=1936-88х²+х^4 4x^2+76=1936-88x^2+x^4 x^4-88x^2-4x^2+1936-76=0 x^4-92x^2+1860=0 Обозначим х^2=у, тогда уравнение примет вид: y^2-92y+1860=0 y1,2=92/2+-√(2116-1860)=46+-√256=46+-16 y1=46+16=62 y2=46-16=30 Подставим данные значения (у) в x^2=y x^2=62 x1,2=+-√62 x1=√62 x2=-√62
Объяснение:
У високостном році 366, є місяці по 31 денів по 30 днів та у лютому 29 днів
Тож подивимось скількі днів у місяці містять двійку:
це номери 2, 12, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29 - загалом це 12 днів на місяць,
як бачимо у кожному місяці високостного року по 12 днів із цифрою 2
тому на рік таких днів буде 12*12=144
а ймовірність такої події
--------------------------
якщо ж казати про можливість натрапити саме на число 2 на листочку то це лише
, оскыльки других днів у році стількиж скіль ки ж і місяців у році, а саме 