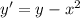
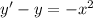
Первый
Решение ищем как сумму общего решения однородного уравнения, соответствующего данному неоднородному, и частного решения данного неоднородного уравнения.
Составим однородное уравнение, соответствующее данному неоднородному:
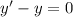
Решаем уравнение с разделяющимися переменными:
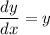
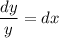
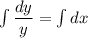
Общее решение однородного уравнения:
Частное решение ищем в виде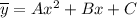 
.
Найдем производную:
Подставим в уравнение:
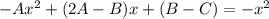
Условие равенства левой и правой частей:
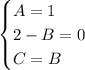
Частное решение неоднородного уравнения:
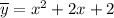
Искомое решение:
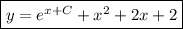
Второй
Решение ищем в виде произведения двух ненулевых функций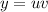 
. Тогда 
.
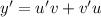Пусть сумма первого и третьего слагаемого в левой части равна нулю:
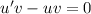
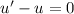
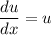
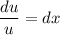
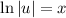
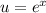
Тогда второе слагаемое в левой части равно правой части:
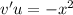
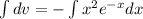
Интеграл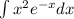 
вычислим отдельно. Будем использовать интегрирование по частям: 
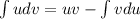(не записывая произвольную константу):
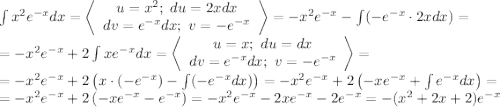
Таким образом:
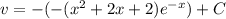
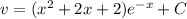
Искомая функция:
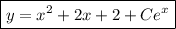
2. 5*4*3 = 60 чисел;
3.
4. 0,04 + 0,1 + 0,2 = 0,34
5. 50/2500 = 0,02 = 2%;
8. Возможных исходов - 6, благоприятных исходов -2. Тогда вероятность равна 2/6 = 1/3;
9.
10. 4*4*3 = 48 чисел;
11.
12. 5/37 = 0,1;
13. В классе 12 + 16 - 25 = 3 ученикв и умные, и красивые. Значит ответ 3/25 = 0,12;
14. 9!/(9-6)! = 9!/3! = 60480;
15.
17. 1/10 = 0,1;
18.
21. х!/((х-1)! * (х - (х-1))!) * (х-1) = х!/(х-1)! * (х-1) = х(х-1) = 30 => х = 6 и х = -5. х = -5 не подходит, так как биноминальные коэффициенты C(n,m) определены при натуральных m,n. Значит х = 6.
22. 17!/(2!*(17-2)!) = 17!/(2!*15!) = 136;
23. Упорядояим ряд: 2,3,3,3,4,4,4,4,5,5.
Медиана равна 4, среднее арифметическое - 3,7.
Модуль разности равен |4 - 3,7| = 0,3;