Дано:
b(n) - геометрическая прогрессия;
b₄ = 8;
b₇ = 512
1) Найти q.
2) Найти n при S(n)=2 ⁵/₈
Решение.
1) Воспользуемся формулой общего члена геометрической прогрессии: 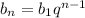
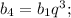
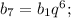
Подставим b₄ = 8; и b₇ = 512 и получим:
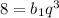 ;
;
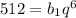
Второе уравнение преобразуем:
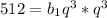
Подставим из первого уравнения 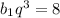 во второе и получим:
во второе и получим:
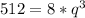
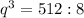
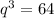
![q=\sqrt[3]{64}](/tpl/images/3193/8714/c03df.png)
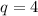
2) Найдем b₁ с первого уравнения:
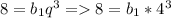
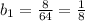
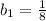
3)Воспользуемся формулой суммы первых членов геометрической прогрессии:
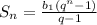
Подставим 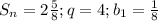
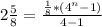
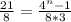
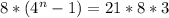
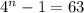
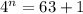
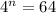
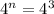
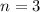
3 перших члена прогресії потрібно взяти, щоб їхня сума дорівнювала
2 ⁵/₈
ответ: 1) q=4;
2) n=3
Проверка:
¹/₈ + ⁴/₈ + ¹⁶/₈ = ²¹/₈ = 2 ⁵/₈
Он обязательно будет лежать в плоскости, перпендикулярной данной, уравнение которой нам нужно составить.
Отложим этот вектор, например, от точки A (-3; 2; 1), т. е. проведём вектор АС, который лежит в искомой плоскости.
Получим точку С (-1; 5; -3), которая тоже лежит в искомой плоскости.
Зная координаты трёх точек A (-3; 2; 1), В (4; -1; 2) и С (-1; 5; -3), лежащих в одной плоскости, найдём уравнение этой плоскости.
Для этого составляем определитель:
| x-(-3) 4-(-3) -1-(-3) |
| y-2 -1-2 5-2 | = 0
| z-1 2-1 -3-1 |
| x+3 7 2 |
| y-2 -3 3 | = 0
| z-1 1 -4 |
Раскрываем определитель по первому столбцу:
(x+3) × |-3 3| - (y-2) × |7 2| + (z-1) × |7 2| = 0
|1 -4| |1 -4| |-3 3|
(x+3) × (-3×(-4)-1×3) - (y-2) × (7×(-4)-1×2) + (z-1) × (7×3-(-3)×2) = 0
(x+3) × (12-3) - (y-2) × (-28-2) + (z-1) × (21-(-6) = 0
(x+3) × 9 - (y-2) × (-30) + (z-1) × 27 = 0
9(x+3) +30(y-2) + 27(z-1) = 0
3(x+3) +10(y-2) + 9(z-1) = 0
3x + 9 + 10y - 20 + 9z - 9 = 0
3x + 10y + 9z - 20 = 0 -- искомое уравнение плоскости