0 это правельно маладеу
Объяснение:
да0
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
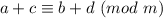
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
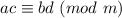
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
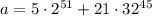
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,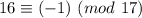 
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что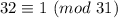 
, получаем
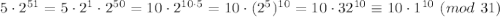
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
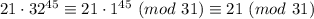
Остаток 21, чудесно. Выполняем последний шаг.
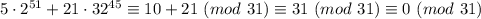
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
Рассмотрим несколько случаем. На месте четной цифры мы будем писать Ч, на месте нечетной - Н. Тот факт, что число нечетное, означает, что последняя цифра у числа нечетная.
1) Число имеет вид ЧЧН. Поскольку на первом месте не может стоять 0, на первое место претендуют 3 цифры - 2, 4, 6. На второе место претендуют 4 цифры - 0, 2, 4, 6 (а если цифры не должны повторяться, то 3 цифры). На третье место претендуют 4 цифры - 3, 5, 7, 9.
Всего получается 3·4·4=48 чисел (при второй интерпретации условия 3·3·4=36 чисел).
2) ЧНН. Здесь аналогично получается 3·4·4=48 чисел (или 3·4·3=36).
3) НЧН. Здесь 4·4·4=64 чисел (или 4·4·3=48).
4) ННН. Здесь 4·4·4=64 числа (или 4·3·2=24)
Суммарно получаем 48+48+64+64=224 чисел - если повторения цифр допускаются (или 36+36+48+24= 144 чисел если все цифры должны быть разные).
Замечание. Если цифры могут совпадать, задачу можно сделать проще . На первом место может стоять любая из цифр, кроме 0 - всего 7 вариантов. На втором месте может стоять любая цифра - всего 8 вариантов. На третьем месте может стоять любая из нечетная цифра - 4 варианта. Всего получаем 7·8·4=224 числа.
ответ: 224 чисел, в которых возможно совпадение цифр, и 144 числа, в которых все цифры разные.
dogfight inductee birdsong grades. song's. essence