1)
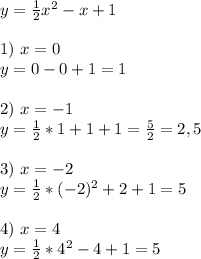
2)
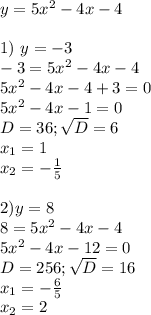
3)
1) y=x²+10 - парабола , поднятая на 10 точек вверх, координаты вершины (0;10)
2) y=x²-5 - парабола, на 5 точек вниз, координаты вершины (0;-5)
3) y=(x+7)² - парабола, передвинутая на 7 точек влево, вершина (-7;0)
4) y=(x-8)²-парабола, передвинутая на 8 точек вправо, вершина (8;0)
4) y=x²
1) y=x²+5
2)y=x²-4
3)y=(x-3)²
4)y=(x+6)²
5)
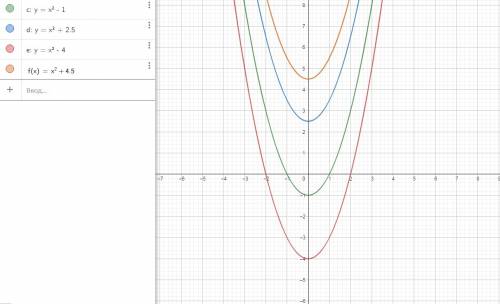
На фото, c Ox пересекается график функции y=x²-4.
Точки пересечения с Ox (-2;0) и (2;0)
И y=x²-1
Точки пересечения с Ox (-1;0) и (1;0)
С Oy : y=x²-1, (0;-1)
y=x²+2,5 , (0;2,5)
y=x²-4, (0;-4)
y=x²+4,5, (0;4,5)
В решении.
Объяснение:
1) Найдите сумму и произведение корней: х² + 7х – 4 = 0.
По теореме Виета:
х₁ + х₂ = -7;
х₁ * х₂ = -4.
2) Одна из сторон прямоугольника на 7 см больше другой, а площадь равна 44 см². Найдите периметр прямоугольника.
х - одна сторона прямоугольника.
(х + 7) - вторая сторона прямоугольника.
Согласно условию задачи уравнение:
(х + 7) * х = 44
х² + 7х - 44 = 0, квадратное уравнение, ищем корни.
D=b²-4ac =49+176=225 √D=15
х₁=(-b-√D)/2a
х₁=(-7-15)/2
х₁= -22/2 = -11, отбрасываем, как отрицательный.
х₂=(-b+√D)/2a
х₂=(-7+15)/2
х₂=8/2
х₂=4 (см) - одна сторона прямоугольника.
4 + 7 = 11 (см) - вторая сторона прямоугольника.
Р = 2(а + в)
Р = 2(11 + 4) = 2 * 15 = 30 (см) - периметр прямоугольника.