x⁵+8x⁴+24x³+35x²+28x+12=0
Следствие из теоремы Безу гласит: "если многочлен с целыми коэффициентами имеет целый корень, то этот корень является делителем свободного члена".
Тогда корень данного уравнения находится среди делителей числа 12, то есть: ±1; ±2; ±3; ±4; ±6; ±12.
Подставляя значения в уравнения, получим, что x=-2 - корень уравнения.
Составим схему Горнера:
| 1 | 8 | 24 | 35 | 28 | 12 |
————————————
-2 | 1 | 6 | 12 | 11 | 6 | 0 |
Теперь можем разложить на множители исходное уравнение:
(x⁴+6x³+12x²+11x+6)(x+2)=0
Далее действия аналогичные:
Находим корень уравнения x⁴+6x³+12x²+11x+6=0 среди делителей его свободного члена: ±1; ±2; ±3; ±6.
Подставляя значения в уравнение x⁴+6x³+12x²+11x+6=0, получим, что x=-2 - корень уравнения.
Составляем схему Горнера:
| 1 | 6 | 12 | 11 | 6 |
—————————
-2 | 1 | 4 | 4 | 3 | 0 |
Теперь получим такое уравнение:
(x³+4x²+4x+3)(x+2)²=0
Находим корень уравнения x³+4x²+4x+3=0 среди делителей его свободного члена: ±1; ±3.
Подставляя значения в уравнение x³+4x²+4x+3=0, получим, что x=-3 - корень уравнения.
Составляем схему Горнера:
| 1 | 4 | 4 | 3 |
———————
-2 | 1 | 1 | 1 | 0 |
Получим такое уравнение:
(x²+x+1)(x+2)²(x+3)=0
x²+x+1=0 или (x+2)²=0 или x+3=0
∅ x=-2 x=-3
ответ: -3; -2.
Вероятность того, что выбранный из 10 юношей окажется одним из двух, имеющим первый дан:
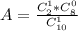
Вероятность того, что выбранная из 4 девушек окажется той единственной. имеющей первый дан:
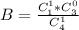
Общую вероятность можно посчитать перемножив вероятность для юношей и для девушек - A*B
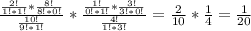
Это если "по-умному". В лоб:
Вероятность выбрать из 10 юношей юношу с первым даном = 2/10, т.к. юношей с первым даном 2, а всего - 10. Для девушек - 1/4. т.к. с первым даном 1, всего - 4. Общая вероятность получается перемножением. ответ такой же: 1/20
По формулам арифметической прогрессии
Количество двузначных четных чисел, кратных 3 (или просто кратных 6)
т = 1 + (96 - 12)/6 = 15
Сумма всех двузначных четных чисел, кратных 3
S = (12 + 96) * 15 / 2 = 810
Двузначные четные числа, кратные 3, но не кратные 7
42 + 84 = 126
Сумма всех четных двузначных чисел кратных 3 но не кратных 7
810 - 126 = 684
Так?