Тут разобрано два варианта, когда требуется найти вероятность, что "хотя бы три детали из пяти дефектные" и когда "ровно три детали из пяти дефектные".
Всего у нас изделий  , изделий имеющих скрытый дефект
, изделий имеющих скрытый дефект 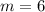 .
.
Выбрать 5 изделий из 18 мы можем 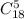
Выбрать три дефектных, мы можем 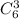 , остальные 2 можем выбрать
, остальные 2 можем выбрать 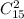
Вероятность события, равна отношению всех исходов к числу благоприятствующих исходов.
 (хотя бы 3 из 5 - дефектные детали)
(хотя бы 3 из 5 - дефектные детали) 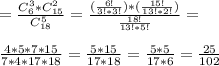
Если в задаче требуется найти вероятность, когда у нас ровно три дефектных изделия, то меняется только количество какими мы можем вытащить оставшиеся две детали, так как нам теперь не нужно учитывать дефектные. Теперь это будет 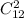
Соответственно:
 (3 из 5 - дефектные детали)
(3 из 5 - дефектные детали) 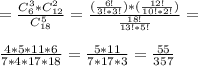
Тут разобрано два варианта, когда требуется найти вероятность, что "хотя бы три детали из пяти дефектные" и когда "ровно три детали из пяти дефектные".
Всего у нас изделий  , изделий имеющих скрытый дефект
, изделий имеющих скрытый дефект 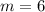 .
.
Выбрать 5 изделий из 18 мы можем 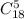
Выбрать три дефектных, мы можем 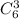 , остальные 2 можем выбрать
, остальные 2 можем выбрать 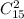
Вероятность события, равна отношению всех исходов к числу благоприятствующих исходов.
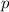 (хотя бы 3 из 5 - дефектные детали)
(хотя бы 3 из 5 - дефектные детали) 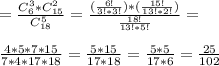
Если в задаче требуется найти вероятность, когда у нас ровно три дефектных изделия, то меняется только количество какими мы можем вытащить оставшиеся две детали, так как нам теперь не нужно учитывать дефектные. Теперь это будет 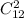
Соответственно:
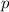 (3 из 5 - дефектные детали)
(3 из 5 - дефектные детали) 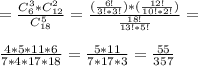
Объяснение:
я сам не знаю но = tgx43