Объяснение:
1) область определения
-х² -2х +3 ≥ 0 ⇒ -3 ≤ х ≤ 1 х ∈ [-3; 1]
функция определена на отрезке [-3; 1]
2) область значений
эта функция задает полуокружность с центром в (-1; 0), радиусом R=2, расположенную выше оси ох
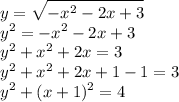
это у нас окружность, но мы искусственно "добавили" отрицательную часть окружности, когда возвели обе части уравнения в квадрат. поэтому наша область значений
0 ≤ у ≤ 2 y ∈ [0; 2]
3) нули
-х² -2х +3 = 0 ⇒ x₁ = -3; х₂ = 1
4) промежутки возрастания/убывания
верхняя точка полуокружности (-1; 2) (-1 получаем из координаты центра, 2 из радиуса) тогда
[-3; -1] функция возрастает
[-1; 1] функция убывает
5) промежутки знакопостоянства
f(x) ≥0
6) минимум и максимум функции
исходя из того, что это полуокружность определенная на отрезке
[-3; 1] с центром в точке (-1,0) и R=2 получим минимум и максимум.
функция достигает:
минимума на концах области определения у(-3) = 0 и у(-1) =0
максимума в верхней точке полуокружности у(-1) = 2
1)=8а²(в²-9с²)=8а²(в-3с)(в+3с).
2)=2(х²-12ху+36у²)=2(х-6у)².
3)=-2а(4а4-4а²+1)= -2а(2а²-1)².
4)=5(а³-8в6)=5(а³-(2в²)³)=5(а-2в²)(а²+2ав²+4в4)
5)=(а³+а²)-(ав-а²в)=а²(а+1)-ав(1+а)=(а+1)(а²-ав)=а(а+1)(а-в)
6)=с4(а-1)-с²(а-1)=(а-1)(с4-с²)=с²(а-1)(с²-1)=с²(а-1)(с-1)(с+1).
1)=(х-у)²-7²=(х-у-7)(х-у+7)
2)=а²-(3в-с)²=(а+3в-с)(а-3в+с)
3)=(в³)²-(2в²-3)²=(в³+2в²-3)(в³-2в²+3).
4)=(m³+3³n³)+(m+3n)²=(m+3n)(m²-3mn+9n²)+(m+3n)²=(m+3n)(m²-3mn+9n²+m+3n).
5)=x²-y²+2x+4y-3=(x²+2x+1)-(y²-4y+4)=(x+1)²-(y-2)²=(x+y-1)(x-y+3).