
пусть масса 3 слитка равна х, а содержание меди в нём у
найдем сколько меди содержится в слитках:
в 1слитке: 5*0,3=1,5 кг
в 2 слитке: 3*0,3=0,9 кг
в 3 слитке (х*у)\100
найдем содержание меди в сплавах:
сплав 1 и 3: (х+5)*0,56=0,56+2,8
сплав 2и 3: (3+х)*0,6=1,8+0,6х
содержание меди в 3 слитке по сплаву 1 и 3: (х+у)\100 = 1,8+0,6х-0,9=0,9+0,6х (1)
содержание меди в 3 слитке по сплаву 2 и 3: (х+у)\100=0,56х+2,8-1,5=0,56х+1,3 (2)
через ур-я (1),(2) выразим х
0,9+0,6х=0,56х+1,3
0,04х=0,4
х=10 кг - масса третьего слитка
из ур-я (1) выразим у:
(х*у)\100=0,56х+1,3, подставим х
10у\100=5,6+1,3
у\10=6,9
у=69% - процент содержания меди в третьем слитке
ответ:10 кг, 69%
1)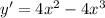
Произведение ранво нулю, когда один из множителей равен нулю.
4x = 0
Имеем три точки экстремума.
2)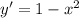
Мы нашли точку экстремума равной -1, которая находится на нашем промежутке. Теперь надо понять, является она максимумом или минимумом. Для этого берем любое значение из промежутка до -1. Например, x = -2, и подставляем в производную.
y'(-2) < 0
Значит на этом промежутке функция убывает, т.е x = -1 это точка минимума.А значит в этой точке функция имеет наименьшее значение на данном промежутке.
Подставляем x = -1 в функцию.
ответ: у = -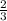
3)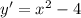
Мы нашли точку экстремума равной 2, которая находится на нашем промежутке. Теперь надо понять, является она максимумом или минимумом. Для этого берем любое значение из промежутка до 2. Например, x = 0, и подставляем в производную.
y'(0) < 0
Значит на этом промежутке функция убывает, т.е x = 2 это точка минимума.А значит в этой точке функция имеет наименьшее значение на данном промежутке. А нам нужно наибольшее значение. Поэтому находим значения функции на границах данного промежутка. Т.е в x = 0 и x = 3.
y(0) =.0
y(3) = 9 - 12 = -3
Получаем, что y(0) > y(3), значит в точке x = 0 функция имеет наибольшее значение на данном промежутке.
ответ: у = 0