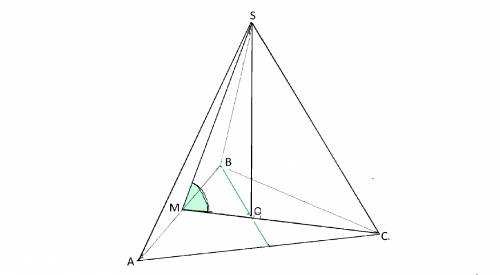
Для того, чтобы ответить на вопрос задания, нужно определиться, что ищем тангенс угла, образованного апофемой SM и высотой MC основания ABC.
Bспомним, что основание высоты правильной пирамиды находится в точке пересечения высот основания, а сама высота перпендикулярна основанию.
Эта точки делит их ( потому что высоты правильного треугольника и медианы и биссектрисы) в отношении 2:1, считая от вершины.
Следовательно, основание О высоты SO пирамиды отстоит от боковой грани на
одну треть высоты MC плоскости правильного треугольника.
Это расстояние 6:3=2
Так как высота пирамиды SO, треть MO высоты основания и апофема SM являются сторонами прямоугольного трегольника SOM,
тангенс угла SMO
между плоскостью боковой грнани и плоскости основания находим отношением противолежащего углу катета к прилежащему.
tg SMO= SO:OM=16:2= 8
Пусть X первый кусок, а Y второй кусок. Тогда после продажи получилось так: первый кусок= X-Y; а второй кусок=Y-0.5*X;
Составим систему (не знаю как нарисовать её, так что образно):
{ X-Y-10=Y-0.5*X; { 1,5X-2Y=10; | *7 { 10,5X-14Y=70;
{ 1,4(X+Y)=91; <=> { 1,4X+1,4Y=91; | *10 <=> { 14X+14Y=910;
{ 24,5X=980; { X=40; { X=40;
{ 1,4X+1,4Y=91; { 1,4Y=35; { Y=25;
ответ: первая ткань 40м, вторая 25м.
h+Rr+r=6+42+7
ответ - в)
Объяснение:
ответ выше, думаю будет так