Вложение............................

Объяснение:
Многочленом стандартного вида называют многочлен, у которого каждый входящий в него член имеет одночлен стандартного вида и не содержит подобных членов
выполним произведение и приведем к стандартному виду
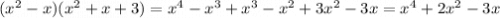
Степенью многочлена называют наибольшую из степеней
входящих в него одночленов
видим, что наибольшая степень это 4
старший коэффициент- это число стоящее перед х в наибольшей степени, в нашем случае коэффициент при x⁴ равен единице
Свободным членом многочлена называют член многочлена стандартного вида без буквенной части
свободного члена в данном многочлене нет
ответ: =40cm2
Объяснение:
Пусть трапеция АВСD, где AD>BC и AD, BC- основания.
Если в трапецию вписана окружность , то суммы противоположных сторон равны.
AB+CD=BC+AD=20
Пусть О центр вписанной окружности, Р точка пересечения диагоналей.
ОМ - радиус окружности , причем так как трапеция равнобочная, то Р лежит на ОМ.
Так как окружность вписанная, то ОМ является половиной высоты трапеции. Продолжим МО до пересечения с AD в точке K.
МК- высота трапеции.
Рассмотрим треугольники APD и CPB. Они подобны по 2-м углам.
( подробно не буду это доказывать, но понятно, что DBC = BDA- накрест лежащие. ). Коэффициент подобия будет равен отношению соответствующих элементов этих треугольников.
Заметим, что КР и МР соответственно высоты треугольников APD и CPB.
Тогда k= KP/MP
Обозначим ОР=3х Тогда ОМ=5х, МР=5х-3х=2х, КР= ОК+ОР=5х+3х=8х
Тогда k= KP/MP =8х/2x=4
Тогда AD:BC=4
=> BC=y => AD=4*y
BC+AD=20 = y+4*y
5*y=20
y=BC=4
AD= BC*k= 4*4=16
Проведем теперь высоту ВН.
АН= (AD-BC):2= (16-4):2=6 cm ( так как трапеция равнобочная)
Тогда из треугольника АВН по т.Пифагора имеем:
ВН= sqrt(BA^2-Ah^2)=sqrt(100-36)=8
S(ABCD)=(AD+BC)*BH/2= 20*8/2=40cm2
То есть k=
1) x(x^2-2)=0
x=0 x^2-2=0
x=+-sqrt(2)
2) 5x^3+5x=0
5x(x^2+1)=0
x=0
3)x(x^3+1)=0
x=0 x=-1
4) x(x^3-8)=0
x=0 x^3=8
x=2
5)2x( 8-x^3)=0
x=0 x=2