Установите соответствие между графиками функций и формулами, которые их задают. Впишите под каждой цифрой букву, соответствующую верной формуле. Формулы: А) у=3х-1 Б) у=-3х-1 В) у=-3х+1 Г) у=3х+1
Решение Пусть х км/ч - скорость второго пешехода. Тогда скорость первого - (х+1) км/ч. Так как встретились пешеходы в 9 км от пункта А, путь первого составил 9 км, а путь второго - 10 км. Значит, второй пешеход провел в пути (10/х) часов, а первый (9/(х+1)+0,5) часов, полчаса из которых потратил на остановку. Составим равнение: 10/x = 9/(x + 1) + 1/2 10/x = (18 + x + 1)/([2*(x + 1)] 20x + 20 = 18x + x² + x x² – x – 20 = 0 x₁ = - 4 не удовлетворяет условию задачи x₂ = 5 5 (км/ч) - скорость второго пешехода 1) 5 + 1 = 6 (км/ч) - скорость первого пешехода ответ: 6 км/ч ; 5 км/ч.
Для решения запишем формулу бинома Ньютона:
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение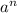
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение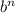
.
Рассмотрим многочлен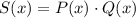
, где:
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена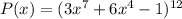
:
- степень определяется выражением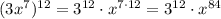
, то есть степень равна 84
- свободный член равен
Для многочлена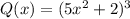
:
- степень определяется выражением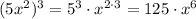
, то есть степень равна 6
- свободный член равен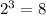
Наконец, для многочлена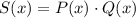
получим:
- степень определяется выражением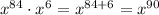
, то есть степень равна 90
- свободный член равен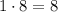
Сумма степени и свободного члена многочлена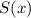
:
ответ: 98