-14
Объяснение:
Условие задачи написано не корректно, то что вы написали можно по разному прочитать, но я всё же думаю, что вы имели в виду это:
(
) * 
.
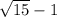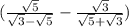С первой скобкой ничего не поделаешь, но во второй скобке можно привести всё к общему знаменателю 
.
() * = () * 
.
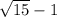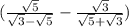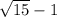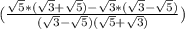Далее во второй скобке раскрываем скобки в числители и знаменателе.
() * = () * 
.
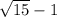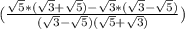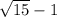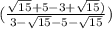Во второй скобке после элементарных арифметических операций получаем:
() * = () * 
.
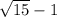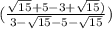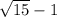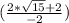Во второй скобке сократим числитель и знаменатель на 2, получаем:
() * = () * 
= () * 
=
= 
= 
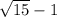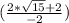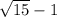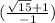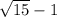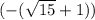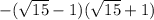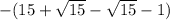= -14.
График функции f(x)=x²+px+q проходит через начало координат
отсюда получаем f(0)=0
или 0=0²+р*0+q
откуда q=0
значит график функции
f(x) имеет вид f(x)=x²+px
Найдем производную f(x)=x²+px
f'(x)=2x+p
Наименьшее значение f(x) будет достигаться в точке Хмин
при f'(Xмин)=0
2Хмин+р=0 откуда Хмин= - р/2 (#)
Нам остаётся найти p
Уравнение касательной к f(x) в точке Хо
у=f(Xo)+f'(Xo)(x-Xo)
f(X0)=Xo²+pXo
f'(Xo)=2Xo+p
значит
у= (Xo²+pXo)+
+(2Xo+p)(х-Хо)=
=(2Xo+p)х+
+(Xo+pXo-2Хо²-pXo)=
=(2Xo+p)х +(-Xo²)
Наша касательная по условию:
y=2х-16
откуда, приравнивая коэффициенты при x и свободные члены, получим :
2Хо+р=2 (1)
-Xo²=-16 и(2)
из (2) получаем Xo²=16 и (Хо)1,2=±4
из (1) находим p=2-2Xo
p1=2-2*4=-6
f1(x)=x²-6x (синий график , см фото)
p2=2+2*4=10
f2(x)=x²+10x (черный график, см фото)
касательная у=2х-16 обозначена красным цветом
из (#)
Хмин= - р/2
подставляем найденные значения p в эту формулу:
(Xmin)1= -(-6)/2=3
(Xmin)2= -10/2=-5
Наименьшие значения функций:
f((Xmin)1)= 3²-6*3=-9
f((Xmin)2)=(-5)²+10(-5)=-25
(два решения)