Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру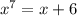 
уравнение в действительных корнях.
Рассмотрим функцию 
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию 
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение 
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
ненулевой остаток от деления на 4 может быть равен 1, 2 или 3.
если при делении на 15 остаток такой же, то и при делении на 60 тоже.
значит, это трехзначное число, которое можно представить как
100a + b + c = 60p + 1; или 60p + 2; или 60p + 3.
так как 60 делится на 10, то c = остатку, 1, 2 или 3.
и это число с есть среднее арифметическое чисел a и b.
если с = 1, то a = b = 1, но число 111 при делении на 60 дает остаток 51.
если с = 2, то а = 3, b = 1, или наоборот, a = 1, b = 3, или a = 4, b = 0.
но числа 132, 312 и 402 тоже не те остатки.
значит, c = 3. тогда возможны такие пары:
(a; b) = (4; 2); (2; 4); (1; 5); (5; 1); (6; 0)
из чисел 420, 240, 150, 510, 600 только 240 и 600 делятся на 60.
ответы: 243 и 603
Зависит от ограничений значений х и у
Объяснение:
Если их нет, то бесконечность