
Можно взять 7 или 8 членов прогрессии
Объяснение:
Дано:
a₂ + a₄ + a₆ = 84
a₄ · a₇ = 196
Sn = 196
Найти:
n
а₁ + d + a₁ + 3d + a₁ + 5d = 84
(a₁ + 3d)(a₁ + 6d) = 196
3a₁ + 9d = 84
a₁² + 9a₁d + 18d² = 196
a₁ = 28 - 3d
(28 - 3d)² + 9d(28 - 3d) + 18d² = 196
784 - 168d + 9d² + 252d - 27d² + 18d² = 196
84d + 588 = 0
84d = - 588
d = -7
a₁ = 28 - 3 (-7) = 49
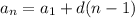
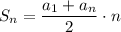
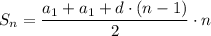
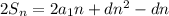
2 · 196 = 2 · 49n - 7n² + 7n
7n² - 105 n + 392 = 0
n² - 15n + 56 = 0
D = 225 - 224 = 1
n₁ = 0.5(15 - 1) = 7
n₂ = 0.5(15 + 1) = 8
можно взять 7 членов прогрессии
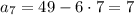
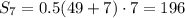
а можно взять и 8 членов прогрессии, так как
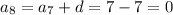
См. Объяснение.
Объяснение:
1) Чтобы раскрыть скобки, надо почленно умножить сомножитель который стоит перед скобкой, на каждое число или буквенное (буквенно-цифровое) выражение, которое стоит в скобках, не забывая при этом о знаках: минус на минус даёт плюс; плюс на минус даёт минус; плюс на плюс даёт плюс:
а · (-36+2с-у)= - 36а + 2ас - ау
Здесь мы сначала а умножили на -36 - получилось - 36а;
затем а умножили на 2с - получилось 2 ас,
затем а умножили на -у - получилось - ау.
2) Здесь всё сделали аналогично:
-1,5 · (2х - 4у) = -3х + 6у
3) А здесь после раскрытия скобок привели подобные:
3·(-4х+6) - (1-12х) = -12х +18 -1 + 12х = 17.
ПРИМЕЧАНИЕ.
В тетради надо записать только решения:
а · (-36+2с-у)= - 36а + 2ас - ау
-1,5 · (2х - 4у) = -3х + 6у
3·(-4х+6) - (1-12х) = -12х +18 -1 + 12х = 17.
Слова писать не надо, т.к. это - объяснение.