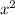-
+ 8х + 3х - 24 = -х (х - 3) + 8 (х - 3) = (х - 3) (8 - х)
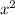- - 11х + 2х + 22 = -х (х + 11) + 2 (х + 11) = (х + 11) (2 - х)
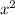- - 17х + 3х + 51 = -х (х + 17) + 3 (х + 17) = (х + 17) (3 - х)
-2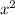 - 22х + 11х + 121 = -2х (х + 11) + 11 (х + 11) = (х + 11) (11 - 2х)
-4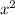 + 10х - 12х +30 = -4х (х + 3) + 10 (х + 3) = (х + 3) (10 - 4х)
-5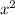 - 10х + 4х + 8 = -5х (х + 2) + 4 (х + 2) = (х + 2) (4 - 5х)
4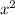 + 16х - 5х - 20 = 4х (х + 4) - 5 (х + 4) = (х + 4) (4х - 5)
9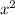 - 27х + 6х + 18 = 9х (х - 3) + 6 (х + 3)
В последнем, скорее всего, какая-то ошибка, потому что преобразовать его в произведение невозможно.
ответ: cos(γ)=0,925, γ≈22°.
Объяснение:
Пусть АВ=2 см, AC=4 см и BC=5 см. Пусть α, β, γ - углы соответственно при вершинах A, B, C треугольника. Для нахождения косинусов углов используем теорему косинусов:
1. BC²=AB²+AC²-2*AB*AC*cos(α), откуда следует уравнение 25=4+16-2*2*4*cos(α), или 25=20-16*cos(α). Отсюда 16*cos(α)=-5 и cos(α)=-5/16. Тогда α=arccos(-5/16)≈108°.
2. AC²=AB²+BC²-2*AB*BC*cos(β), откуда следует уравнение 16=4+25-2*2*5*cos(β), или 16=29-20*cos(β). Отсюда 20*cos(β)=13 и cos(β)=13/20. Тогда β=arccos(13/20)≈49°.
3. AB²=AC²+BC²-2*AC*BC*cos(γ), откуда следует уравнение 4=16+25-2*4*5*cos(γ), или 4=41-40*cos(γ). Отсюда 40*cos(γ)=37 и cos(γ)=37/40. Тогда γ=arccos(37/40)≈22°
Проверка: сумма углов треугольника должна быть равна 180°. В нашем случае α+β+γ≈108°+49°+22°=179°≈180°, так что углы найдены верно.
Таким образом, наименьшим углом является γ. Его косинус равен 37/40=0,925, а его градусная величина - ≈22°.
1) x∈ (-∞; +∞)
2) x∈∅
Объяснение:
1) 4x +31 - 10x - 11 = 7 +13 - 6x
-6x +20 = 20 - 6x
При любом X, x∈ (-∞; +∞)
2) 8x +11 - 13 = 13x-5x -5
8x-2 = 8x-5
Нет решений
x∈∅