ab - ac - 4b + 4c = a(b - c) - 4(b - c) = (b - c)(a - 4).
Как выполняется: ищем что-то одинаковое у нескольких слагаемых. Так, мы увидели одинаковый сомножитель a в слагаемых ab и -ac, одинаковый сомножитель 4 у слагаемых -4b и 4c. Вынесли их за скобку и заметили, что появились две одинаковые скобки: (b - c) – которые являются сомножителями для a(b - c), -4(b - c). Выносим за скобку его и получаем разложение.
То есть вам нужно найти что-то одинаковое у нескольких слагаемых и вынести это за скобку.
ответ: (b - c)(a - 4).
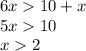
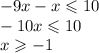

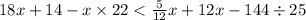
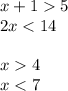
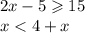
1)tg^2(a)+sin^2(a)-1/(cos^2(a))=sin^2(a)/cos^2(a)+sin^2(a)-1/cos^2(a)=(sin^2(a) - sin^2(a)-cos^2(a)+sin^2(a)*cos^2(a))/cos^2(a)=(cos^2(a)(sin^2(a)-1))/cos^2(a)= sin^2(a)-1= sin^2(a)- sin^2(a)-cos^2(a)= -cos^2(a)
2)(cos(3 a)+cos(a))/(2 cos(a))+2 sin^2(a)=((4cos^3(a)-3cos(a)+cos(a))/2cos(a))+2sin^2(a)= ((4cos^3(a)-2cos(a))/2cos(a))+2sin^2(a)=2cos(a)*(2cos^2(a)-1)/2cos(a)+2sin^(a)=2cos^2(a)-cos^2(a)-sin^2(a)+2sin^2(a)=cos^2(a)+sin^2(a).