Левая часть представляет собой сумму неотрицательных слагаемых, эта сумма обращается в ноль тогда и только тогда, когда оба слагаемых суть нули, если хоть одно из них отлично от нуля, то вся сумма (левая часть) отлична от нуля (больше нуля). Таким образом данное уравнение равносильно системе: { (x^2-1)^2 = 0; { (x^2 - 6x -7)^2 = 0; что равносильно { x^2-1 = 0; { x^2 - 6x - 7 = 0; равносильно { x^2=1; {x^2 - 6x - 7 = 0; первое уравнение дает x1=1; или x2=-1; x1 = 1, подставляем во второе уравнение последней системы: 1 - 6 - 7 = 0; <=> -12=0, ложное равенство, поэтому x1=1, не является решением системы. x2 = -1; подставляем во второе уравнение: (-1)^2 - 6*(-1) - 7 = 1+6-7=0, верное равенство, таким образом x=-1 единственное решение системы. ответ. x=(-1).
Здесь используются перестановки с повторениями. Допустим, есть группа из n различных элементов. Тогда количество их расставить на n мест равно n!. Теперь пусть внутри группы из n элементов есть повторяющиеся элементы. Допустим, есть k_1 элементов, равных a_1; k_2 элементов, равных a_2; ... ; k_q элементов, равных a_q. Выполняется условие k_1 + k_2 +..+k_q = n. Тогда число РАЗЛИЧНЫХ расставить n уже не различных элементов на n мест равно n!/(k_1! * k_2! * ... * k_q!). Применим эту формулу к этой задаче. Будем отталкиваться от количества 1 и 4. Пусть оно равно k. 1) k = 0. Тогда имеется 1 группа с 5 элементами, равными 7, а количество расставить их на 5 мест равно 5!/5! = 1. 2) k = 1. Тогда имеется 3 группы: 1-я группа состоит из одного элемента 1, 2-я группа состоит из одного элемента 4, 3-я группа состоит из трех элементов 7. Тогда число расставить их равно 5!/(1!*1!*3!)=20. 3) k = 2. Имеется 3 группы: 1-я группа состоит из двух элементов, равных 1, 2-я группа состоит из двух элементов, равных 4, третья группа состоит из одного элемента, равного 7. Тогда число расставить их равно 5!/(2!*2!*1!)=30. Случаи с k > 2 невозможны, так как в пятизначном числе не может быть одновременно k > 2 единиц и четверок. Суммируем полученные
Используем n-ый член геометрической прогрессии: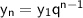
Первый член: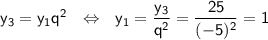
Найдем члены с первого по шестой