"Какое из неравенств верно, если a < 0, За+b/b=2?
a)b<a<0 , b)a<b<0 ,c)a<0<b ,d)0<b<c ,e)b<c<0. "
Объяснение:
Условие За+b/b=2, очевидно (За+b) /b=2 ⇒ 3а/в+в/в=2 ,3а/в+1=2,
3а/в=1 , 3а=в. Т.к. 3>0 , a<0 , то 3a<0 . Поэтому в<0. Если расположить их на оси :
_ _ _ _ _ (в=3а)_ _ _ _ _ _ _(а)_ _ _ _ _ (0) + + + + +
За+b/b=2?
a)b<a<0 верно, т.к отрицательное в=3а лежит на оси левее а;
b)a<b<0 неверно (см чертеж);
c)a<0<b неверно;
d)0<b<c НЕЛЬЗЯ дать достоверный ответ( нет данных) ;
e)b<c<0 НЕЛЬЗЯ дать достоверный ответ( нет данных) .
ответ получается 2 см^2
Объяснение:
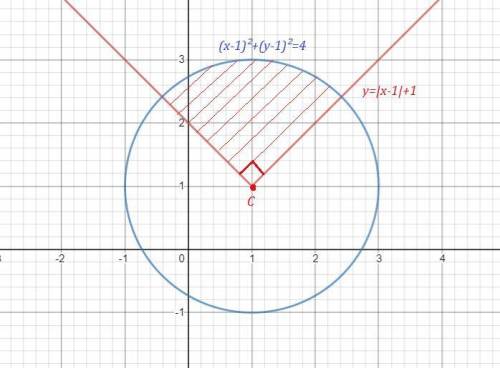
Мы должны понять, что это за графики
(1) Это график с модулем
(2) Это график окружности
Т.к. это система неравенства мы эти оба графика соединяем в один и смотрим пересечение.
У нас сначала получился сектор, но т.к. сказано найти фигуру, то мы проводим хорду, которая будет являться гипотенузой равнобедренного(он равнобедренный из-за того, что его катеты это радиус окружности) прямоугольного треугольника. Этот равнобедренный прямоугольник треугольник входит в сектор, который является промежутком этой системы неравенства.
По формуле окружности можно понять что R=2 см
Площадь тогда будет S= 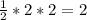 см^2
см^2
13x-13y+x=-xy
dy/dx=-y+14/-13+x