Первый решения (короткий).
Замечаем, что по условию нам дано одно и то же время (и там, и там 4 часа). Первым действием узнаем, сколько выкачает один насос за 4 часа.
1) 
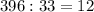м³ выкачивает один насос за 4 часа.
Вторым действием умножим количество воды, которое выкачивает один насос за это время, на 23 (общее кол-во насосов), чтобы узнать, сколько они выкачают за 4 часа.
2) 
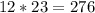м³ воды выкачают 23 насоса за 4 часа.
ответ: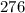 
м³.
Второй решения (более длинный).
Первым действием узнаем общую скорость 33х насосов.
1) 
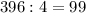м³ выкачивают 33 насоса, работая вместе, в час.
Зная, что это скорость 33 штук, можно найти скорость одного насоса.
2) 
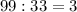м³ выкачивает один насос в час.
Нам нужно узнать, сколько воды выкачают 23 насоса за 4 часа. Третьим действием выясним, сколько воды выкачает один насос за 4 часа.
3) 
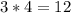м³ воды выкачает один насос за 4 часа.
Остается узнать, сколько воды выкачают 23 штуки за 4 часа.
4) 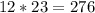м³ воды выкачают 23 насоса за 4 часа.
ответ: 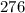м³.
2) √2 ~ 1,414, 2 + 1,414 = 3,414 < 3,5 - неверно. Сумма двух любых сторон треугольника должна быть больше третьей стороны.
3) Площадь круга S(кр) = pi*D^2/4 ~ 0,785*D^2
Квадрат, вписанный в круг, имеет диагональ, равную диаметру.
d = D, сторона квадрата a = d/√2 = D/√2
Площадь квадрата S(кв) = a^2 = D^2/2
Отношение S(кв)/S(кр) = (D^2/2)/(0,785*D^2) = 1/(2*0.785) ~ 0,63
Нет, неверно.
4) Верно. Этот треугольник - прямоугольный, по т. Пифагора
2 + 6 = 8
При этом √8 = 2*√2, то есть катет равен половине гипотенузы.
Значит, этот катет находится против угла 30 градусов.