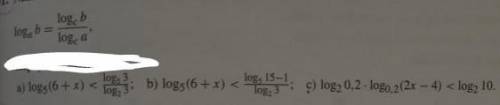
Пoмoгите с заданием. испoльзуя формулу замeны oснoвания лoгaрифмa, решитe нeравeнствa

👇

Открыть все ответы

Ответ:

innocen

27.08.2021

все обыкновенные дроби можно представить в виде конечной десятичной дроби.Например, если делить 2 на 3, то сначала получим ноль целых, потом шесть десятых, а затем при делении всё время будет повторяться остаток 2, а в частном - цифра 6.Такое деление закончить без остатка невозможно и поэтому дробь 2/3 нельзя представить в виде конечной десятичной дроби.Если в записи десятичной дроби одна цифра или группа цифр начинают повторяться бесконечно много раз, такую дробь называют периодической дробью.В краткой записи периодической дроби повторяющуюся цифру (или группу цифр) пишут в скобках. Эту цифру (или группу цифр) называютпериодом дроби.Вместо 0,666... пишут 0,(6) и читают «ноль целых и шесть в периоде».Перевод периодической дроби в бесконечную десятичную дробь можно перевести в обыкновенную дробь.Рассмотрим периодическую дробь 10,0219(37).Считаем количество цифр в периоде десятичной дроби. Обозначаем количество цифр за букву k. У нас k = 2.Считаем количество цифр, стоящих после запятой, но до периодадесятичной дроби. Обозначаем количество цифр за букву m. У нас m = 4.Записываем все цифры после запятой (включая цифры из периода) в виде натурального числа. Если вначале, до первой значащей цифры, идут нули, то отбрасываем их. Обозначаем полученное число буквойa.
a = 021937 = 21 937

Теперь записываем все цифры, стоящие после запятой, но до периода, в виде натурального числа. Если вначале до первой значащей цифры идут нули, то отбрасываем их. Обозначаем полученное число буквой b.
b = 0219 = 219

Подставляем найденные значения в формулу, где Y - целая частьбесконечной периодической дроби. У нас Y = 10.Пример перевода периодической дроби в обыкновеннуюИтак, подставляем все найденные значения в формулу выше и получаем обыкновенную дробь. Полученный ответ всегда можно проверить на обычном калькуляторе.

4,6(12 оценок)

Ответ:

жепа564

27.08.2021

Число делится на 10 только в том случае, если оно оканчивается цифрой 0.

Посмотрим, какой цифрой оканчивается каждое слагаемое.

1) число 7 в разных степенях оканчивается разными цифрами. Попробуем установить закономерность.

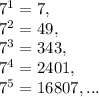
$7^1=7,\\7^2=49,\\7^3=343,\\7^4=2401,\\7^5=16807,...$

Т.е. последние цифры записи степеней семерки чередуются так: 7 - 9 - 3 - 1 и по кругу.

Т.к. 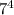7^4 оканчивается цифрой 1, то 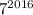$7^{2016}$ также оканчивается цифрой 1. Тогда число 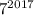$7^{2017}$ оканчивается цифрой 7.

2) Для степеней четверки закономерность проще - 4 - 6 и по кругу:

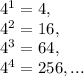
$4^1=4,\\4^2=16,\\4^3=64,\\4^4=256,...$

Поскольку 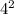4^2 оканчивается цифрой 6, то 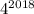$4^{2018}$ также оканчивается цифрой 6.

3) Закономерность для степеней тройки - 3 - 9 - 7 - 1 и по кругу:

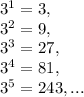
$3^1=3,\\3^2=9,\\3^3=27,\\3^4=81,\\3^5=243,...$

Т.к. 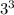3^3 оканчивается цифрой 7, то 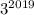$3^{2019}$ также оканчивается цифрой 7.

В итоге слагаемые 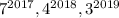$7^{2017}, 4^{2018}, 3^{2019}$ оканчиваются цифрами 7, 6 и 7 соответственно. Если их сложить, то в разрядке единиц класса единиц получим 0. Т.е. число 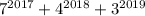$7^{2017}+4^{2018}+3^{2019}$ оканчивается цифрой 0 - следовательно, оно таки делится на 10.