Вычислить: а)0,5√0,04+1/6 √144; б)2√(9/16)-1; в)(2√0,5)^2. ( )
Найдите значение выражения:
а)√(0,36∙49); б)√24∙√6; в)√27/√3. ( )
Упростите выражение:
а)10√3-√48-√75; б)(√2-√18)∙√2; в)(3-√5)^2. ( )
Внесите множитель под знак корня и сравните:
а)7√2 и √99; б)6√2 и √70. ( )
Решить уравнение:
а) х2 = 5; б) х2 = - 3; в) 100х2 – 16 = 0.

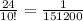

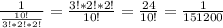
ОДЗ:
{10-x²-1≥0 ⇒ 9-x²≥0 _-_[-3]_+_[3]_-_ ⇒ -3≤x≤3
cos(2x+(π/2))=0
2x+(π/2)=(π/2)+πk, k∈Z
2x=πk, k∈Z
x=(π/2)·k, k∈Z
Найдем корни удовлетворяющие неравенству -3≤x≤3:
-3 ≤ (π/2)·k ≤ 3, k∈Z;
-2< -6/π ≤ k ≤ 6/π<2- неравенство верно при k=-1; k=0; k=1.
x=-π/2; x=0; x= π/2 - корни уравнения.
√(10-х²-1)=0 ⇒ х=-3 или х=3
х=-3; х=3 - корни уравнения.
О т в е т. -3;-π/2; 0; π/2; 3.