<var>(x−5)
2
=5x
2
−(2x−1)(2x+1)</var>
< var > x^{2}-10x+25=5x^{2}-(4x^{2}-1) < /var ><var>x
2
−10x+25=5x
2
−(4x
2
−1)</var>
< var > x^{2}-10x+25=5x^{2}-4x^{2}+1 < /var ><var>x
2
−10x+25=5x
2
−4x
2
+1</var>
< var > x^{2}-10x+25=x^{2}+1 < /var ><var>x
2
−10x+25=x
2
+1</var>
< var > x^{2}+1-x^{2}+10x-25=0 < /var ><var>x
2
+1−x
2
+10x−25=0</var>
< var > (x^{2}-x^{2})+10x+(1-25)=0 < /var ><var>(x
2
−x
2
)+10x+(1−25)=0</var>
< var > 10x-24=0 < /var ><var>10x−24=0</var>
< var > 10x=24 < /var ><var>10x=24</var>
< var > x=24:10 < /var ><var>x=24:10</var>
< var > x=2,4 < /var ><var>x=2,4</var>
< var > (2,4-5)^{2}=5\cdot(2,4)^{2}-(2\cdot2,4-1)\cdot(2\cdot2,4+1) < /var ><var>(2,4−5)
2
=5⋅(2,4)
2
−(2⋅2,4−1)⋅(2⋅2,4+1)</var> (это проверка)
< var > (-2,6)^{2}=5\cdot5,76-(4,8-1)\cdot(4,8+1) < /var ><var>(−2,6)
2
=5⋅5,76−(4,8−1)⋅(4,8+1)</var>
< var > 6,76=28,8-3,8\cdot5,8 < /var ><var>6,76=28,8−3,8⋅5,8</var>
< var > 6,76=28,8-22,04 < /var ><var>6,76=28,8−22,04</var>
< var > 6,76=6,76 < /var ><var>6,76=6,76</var>
Объяснение:
1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.
В примере в) коэффициенты k=5, значит их графики параллельны.
2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.
3. АБВГ
2413
4. 2x + y = 8
2x - y = 1
Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:
2x - (8 - 2x) = 1
2x - 8 + 2x = 1
4x = 9
x = 2,25
y = 8 - 2*2,25 = 8 - 4,5 = 3,5
ответ: (2,25; 3,5)
5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.
2)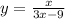 . Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
. Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
б) при
при 
Если x = -5, то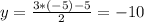
Если х= 3, то
Значит,