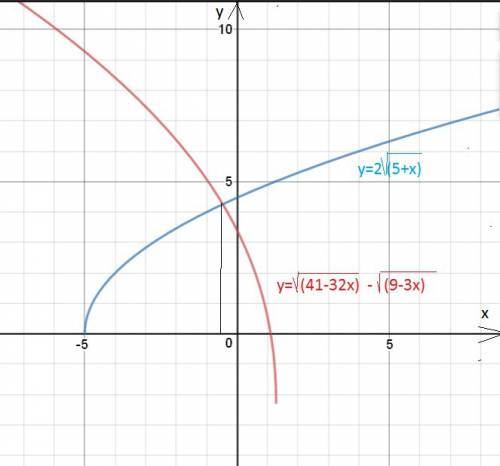
41-32х≥0;
9-3х≥0
5+х≥0
ОДЗ: х ∈[-5; 41/32]
Перепишем уравнение в виде
√(41-32x)=2√(5+x)+√(9-3x)
Возводим в квадрат.
41-32х=4(5+х)+4√(5+х)·√(9-3х)+9-3х
4√(5+х)·√(9-3х)=12-33х
Возводим в квадрат при условии 12-33х≥0 ⇒ х ≤12/33.
16(5+х)(9-3х)=144-792х+1089х²;
1137х²-696х-576=0
379х²-232х-192=0
D=(-232)²-4·379·(-192)=53 824+291 072=344 896
x=(232-√344896)/758≈-0,47 или х=(232+√344896)/758≈1,08 - не удовлетворяет условию х ≤12/33, поэтому не является корнем уравнения
Дано: ABC - равнобедренный треугольник; AC = 12 см; AD = 9.6 см; AB=BC.
Найти: Рabc.
Из прямоугольного треугольника ADC по теореме Пифагора найдем CD
Пусть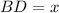
, тогда 
.
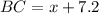Рассмотрим прямоугольный треугольник BHC найдем высоту BH к стороне основания AC; AH=CH=AC/2=6 см.
Площадь равнобедренного треугольника равна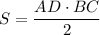
, с другой стороны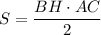 
Приравнивая площади, получим AD * BC = BH * AC.
После возведения в квадрат обе части уравнения и упрощений с подобными членами вы должны получить следующее квадратное уравнение
Корни которого:
- не удовлетворяет условию
Тогда
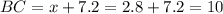см
Pabc = AB + BC + AC = 10 + 10 + 12 = 32 см
ответ: 32 см.