y = x³ - 4x²
Найдём производную :
y' = (x³)' - 4(x²)' = 3x² - 8x
Найдём критические точки, для этого приравняем производную к нулю.
y' = 0
3x² - 8x = 0
x(3x - 8) = 0
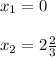
Отметим критические точки на числовой прямой и выясним знаки производной на промежутках, на которые эти точки разбивают числовую прямую .
y'(x) + - +
____________0___________2 2/3_____________
y(x) ↑ ↓ ↑
На промежутках (- ∞ ; 0] и [2 2/3 ; + ∞) -функция возрастает
На промежутке [0 ; 2 2/3] - функция уюывает
Объяснение:
5) |10x - 71| - 32 = -16;
|10x - 71| = -16+32
|10x - 71|=16
10х-71=16
10х-71=16 10х-71=-16
10х=71+16 10х=71-16
х=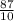 х=
х=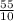 =
=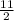
4)|8 - 0,2x| = 12;
|8 - 0,2x| = 12;
8-0,2х=12 8-0,2х=-12
-0,2х=12-8 -0,2х=-12-8
-0,2х=4 -0,2х=-20
х=4÷(-0,2) х= (-20)÷(-0,2)
х= -20 х=100
6) | | x| - 2| = 2.
| x| - 2 = 2
| x| - 2 = -2
х=4
х=-4
х=0