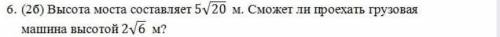
Нужно сравнить два числа 5√20 м и 2√6 м. Так как оба числа положительные, то можно сравнить квадраты этих чисел.
5√20 = 10 √5 = 22,36
2√6 = 4,89 ⇒
5√20 > 2√6 ⇒
Высота моста больше высоты грузовой машины
ответ : Да, сможет.
Решение системы уравнений t₁=0 t₂=1
z₁=1 z₂=2
Объяснение:
Реши систему уравнений:
{t²−z=−1
{t−z+1=0
Выбери пары чисел, которые являются решением системы уравнений:
t=0,z=1
t=1,z=2
t=0,z=3
t=1,z=1
другой ответ
Выразим z через t в первом и втором уравнениях, приравняем правые части (левые равны) и вычислим t:
-z= -1-t²
-z= -1-t
z=t²+1
z=t+1
t²+1=t+1
t²+1-t-1=0
t²-t=0
t(t-1)=0
t₁=0 z₁=0+1=1
t-1=0
t₂=1 z₂=1+1=2
Решение системы уравнений t₁=0 t₂=1
z₁=1 z₂=2
Задача имеет 2 решения
A(5;5) C(-5;-5) или A(-5;-5) C(5;5)
Объяснение:
Введу обозначение-(MN) это вектор MN
Точки B(−5; 5) и D(5; −5) центрально симметричны относительно начала координат О(0; 0), что совпадёт с центром симметрии квадрата. Значит и точки А и С симметричны относительно относительно точки О.
Пусть координаты точки А(x; y), тогда координаты точки С(-x; -y)
AC²=(-x-x)²+(-y-y)²==4x²+4y²
BD²=(-5-5)²+(-5-5)²=200
AC²=BD²
4x²+4y²=200
x²+y²=50
(CA)⊥(BD)⇒(AC)·(BD)=0
(CA)={2x;2y}; (BD)={10;-10}
0=(AC)·(BD)=10·2x+(-10)·2y=20x-20y⇒x-y=0⇒y=x
x²+x²=50
2x²=50
x²=25
x=±5⇒y=x=±5
A(5;5) C(-5;-5) или A(-5;-5) C(5;5)
Объяснение:
надо сравнить эти числа,для этого внесем множитель под знак корня
5√20=√5²*20=√25*20=√500
2√6=√2²*6=√4*6=√24
2√6м=√24 м < 5√20м=√500 м значит грузовая машина может проехать под этим мостом