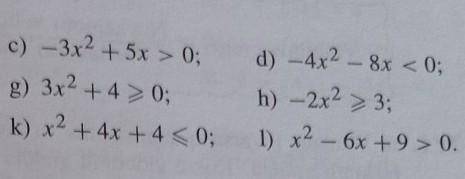
1) Если после переливания 12,5% содержимого первого бидона во второй их содержимое уравняется, то аналогичное будет после переливания 25% из первого бидона в третью емкость.
Следовательно, если содержимое первого бидона принять за Х, то содержимое второго бидона 0,75 * Х. Получаем уравнение
Х + 0,75 * Х = 1,75 * Х = 70 , откуда Х = 40.
Итак, в первом бидоне 40 л молока, а во втором - 30 л.
2) Если собственная скорость катера Х км/ч, то его скорость по течению
Х + 3, а против течения - Х - 3. Получаем уравнение
5 * (Х + 3) + 3 * (Х - 3) = 5 * Х + 15 + 3 * Х - 9 = 8 * Х + 6 = 126 , откуда Х = 15 , следовательно, собственная скорость катера 15 км/ч
3x²- 5x - 2 = 0,
Д = (-5)² - 4*3*(-2) = 25 + 24 = 49 ⇒ 2 корня, так как Д >0,
4х² - 4х + 1 = 0,
Д = (-4)² - 4*4*1 = 16 - 16 = 0 ⇒ 1 корень, так как Д = 0,
х² - 2x +3 = 0,
Д = (-2)² - 4*1*3 = 4 - 12 = -8 ⇒ корней нет, так как Д < 0,
х² - 8х + 15 = 0,
Д = (-8)² - 4*1*15 = 64 - 60 = 4,
х1 = (8 + 2) / 2*1 = 10/2 = 5,
х2 = (8 - 2) / 2*1 = 6/2 = 3,
4х² - 40х + 25 = 0,
Д = (-40)² - 4*4*25 = 1600 - 400 = 1200, ( √1200 = √(3*400) = 20√3 ),
х1 = (40 + 20√3) / 2*4 = 5(2 + √3)/2,
х1 = (40 - 20√3) / 2*4 = 5(2 - √3)/2,
х² - х + 7 = 0,
Д = (-1) - 4*1*7 = 1 - 28 = -27 ⇒ корней нет (Д < 0)
ответ:в g) любое число, от минус бесконечности до плюс, т к квадрат положителен всегда. В k) x<-2
Объяснение: