35 км/ч
Объяснение:
Дано:
S₁ = 35 км
S₂ = 34 км
t = 2 ч
Vр = 1 км/ч
V - ?
1)
Заметим, что собственная скорость лодки равна скорости ее движения по озеру:
V₁ = V
Время, затраченное на движение по озеру:
t₁ = S₁ / V₁
или
t₁ = S₁ / V.
2)
Время, затраченное на движение по реке.
Заметим, что река впадает в озеро, а это значит, что лодка двигалась против течения: V₂ = V - Vp
t₂ = S₂ / V₂ или
t₂ = S₂ / (V - Vp)
3)
Общее время движения:
t = t₁ + t₂
или
t = S₁ / V₁ + S₂ / (V - Vp)
Подставляем данные и решаем уравнение:
2 = 35 / V + 34 / (V - 1)
2·V·(V-1) = 35·(V-1) + 34·V
2·V² - 2·V = 35·V - 35 +34·V
2·V² - 71·V + 35 = 0
Решая это квадратное уравнение, получаем:
V = (71-69)/4 = 0,5 км/ч (слишком маленькая скорость...)
V = (71+69)/4 = 35 км/ч
Для того чтобы решить дробно-рациональное уравнение нужно все перенести в левую часть, оставив в правой части лишь 0
Приводим все к одному знаменателю. Для этого достаточно умножить х на знаменатель 7-х. Получается:
Когда дробь равна нулю? Когда числитель равен нулю, а знаменатель не равен нулю. Значит пишем:
Решаем квадратное уравнение и обычное неравенство. Получаем значения:
x=3, х=4 и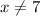
В ответ пишем только ответы числителя, если они не совпадают с ответами знаменателя. Если совпадают, то их нельзя писать, т.к. при этих значениях дробь не имеет смысла, потому что на ноль делить нельзя. Т.е. если бы у нас в квадратном уравнении получился еще ответ х=7, то мы бы его в ответ не записывали по указанным ранее причинам. Но в нашем случае никаких совпадений нет, поэтому пишем:
ответ: х=3 и х=4