О данном животном было упомянуто в книге “Индика”. К сожалению, труды врача не дошли до наших дней, но существует большое количество произведений других авторов, которые опирались на суждения Ктесия. Необходимо сказать, что благодаря этому врачу грекам стали известны многие мифические существа. Более ясное описание о животном сложилось только ко 2 веку до нашей эры, его сделал Клавдий Элиан. Но существовали и деятели, которые не верили в мантикору. Так, греческий географ Павсаний не признавал эти писания про мифическое животное и говорил, что это
Источник: https://mifistoria.info/mantikora
f(x) = 5 +2x - 3
f(x) = 2x + 2
Есть несколько начертить этот график, но в конечном итоге получается одно и то же. Мне больше нравится этот:
1) Строим график функции f(x) = x. Это будет прямая, построенная под углом 45° к оси Ох (пунктирная линия на графике)
2) Теперь строим график функции f(x) = 2x путём сжатия исходного графика к оси Оу. Выглядит это так (прямая, выходящая из начала координат, которая не пунктирная).
3) Ну и наконец, смещаем полученный график на 2 единицы вверх (прямая, выходящая из точки 2 на оси Оу, самая тёмная на рисунке)
Когда разберётесь с этим, можно опускать эти пункты и сразу строить конечный, но на первых порах лучше максимально разобрать этот процесс
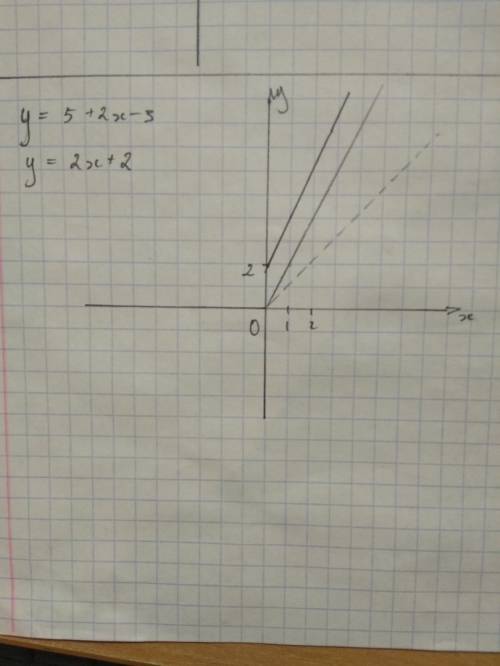
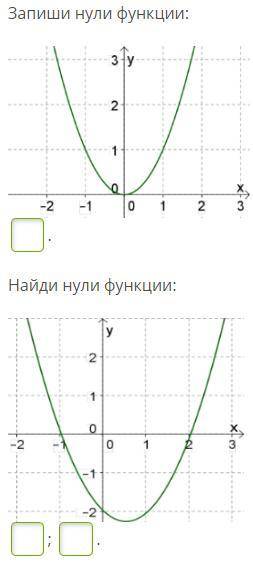
В решении.
Объяснение:
Нули функции - это абсциссы (значения х) точки пересечения графиком оси Ох, где у всегда равен нулю.
На первом графике ветви параболы не пересекают ось Ох, а только соприкасаются, координаты нуля функции (0; 0); абсцисса = 0;
На нижнем графике есть две точки пересечения параболой оси Ох, координаты нулей функции (-1; 0); (2; 0); абсциссы: -1; 2.