 .
. .
. .
.
 . Но
. Но  фактически лишнее неравенство, оно выполняется автоматически потому, что
фактически лишнее неравенство, оно выполняется автоматически потому, что 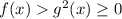 , ибо полный квадрат всегда неотрицателен.
, ибо полный квадрат всегда неотрицателен.
 .
. .
. .
.
 . Но
. Но  фактически лишнее неравенство, оно выполняется автоматически потому, что
фактически лишнее неравенство, оно выполняется автоматически потому, что 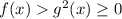 , ибо полный квадрат всегда неотрицателен.
, ибо полный квадрат всегда неотрицателен.
По признаку Коши исследуем. Не забыть писать не х, а |x|/
lim√(4n+1/n+7)^n *|x|^n =lim (4n+1/n+7)*|x|=4*|x| (корень только не квадратный, а n-ой степени)
4*|x|<1
-1/4<x<1/4