y=(x-6)^2*(x-3)+3
y'=[ (x-6)^2*(x-3) ] ' = ((x-6)^2)' *(x-3)+(x-6)^2*(x-3)' = 2*(x-6)(x-3)+(x^2-6)=(x-6)(3x-12)
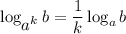 имеем , что
имеем , что 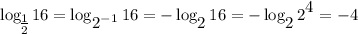
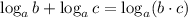 , получим что
, получим что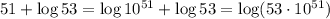
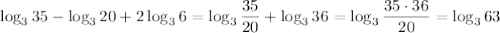
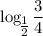 и
и 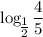
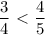 , то в силу монотонности функции(
, то в силу монотонности функции(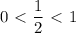 функция убывающая) имеем что
функция убывающая) имеем что 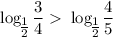
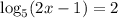
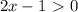 откуда
откуда 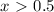
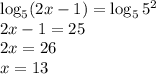
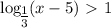
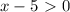 откуда
откуда 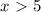
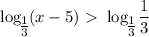
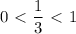 , функция убывающая, то знак неравенства меняется на противоположный
, функция убывающая, то знак неравенства меняется на противоположный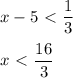
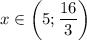
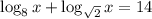
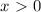
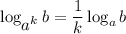 , получим что
, получим что
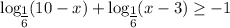
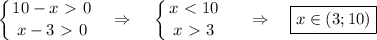
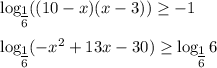
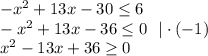
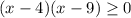 (*)
(*)![x \in (-\infty;4]\cup[9;+\infty)](/tpl/images/0366/9080/721ac.png)
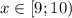 - ОТВЕТ.
- ОТВЕТ.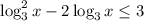
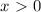
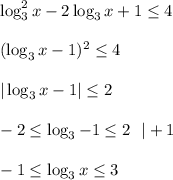
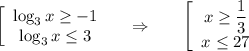
![x \in \bigg[\dfrac{1}{3} ;27\bigg].](/tpl/images/0366/9080/7e293.png)
y'=2(x-6)*(x-3)+(x-6)^2*1+0=(x-6)(2x-6+x-6)=(x-6)(3x-12)
Когда нужно найти производную произведения, то делают так: производная первого выражения * просто второе выражение + просто первое выражение * производную второго, т.е. (yg)'=y'g+yg'